题目内容
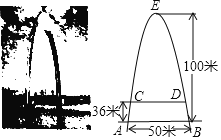
【题目】如图所示是某斜拉索大桥,主索塔呈抛物线,主索塔底部在水面部分的宽度AB=50米,主索塔的最高点E距水面的垂直距离为100米,桥面CD距水面的咨度为36米,则桥的宽度CD_____米.
【答案】40.
【解析】
以CD所在直线为x轴,过点E的直线为y轴建立平面直角坐标系,根据图象知顶点E的坐标为(0,64),点B的坐标为B(25,-36),确定函数的解析式后即可求得线段CD的长.
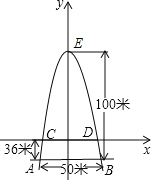
如图,以CD所在直线为x轴,过点E的直线为y轴建立平面直角坐标系,
根据图象知点顶点E的坐标为(0,64),点B的坐标为B(25,﹣36),
设解析式为y=ax2+64,
将点B(25,﹣36)代入得:﹣36=625a+64,
解得:a=﹣![]() ,
,
∴解析式为y=﹣![]() x2+64,
x2+64,
令y=0,得:y=﹣![]() x2+64=0,
x2+64=0,
解得:x=±20,
∴CD=20﹣(﹣20)=40,
故答案为:40.

练习册系列答案
相关题目