��Ŀ����
����Ŀ�����ػƶ�������������ݮ��һ����������������Ŀǰ�������γ��������ַ�������ģ��ֲ�����в�ժ��Ԥ�䱣�ʡ�ʳƷ�ӹ��Ƚ�Ϊ��������ݮ��ҵ.ij��ݮ��ֲ�������ز�����������ժ����ݮ���ּӹ����ۣ�����ֱ�����ۣ��ҵ��춼�������ֱ꣬��������40Ԫ/��ӹ�������130Ԫ/��(�������) ��֪���ع�Ӷ20�����ˣ�ÿ������ֻ�ܲ����ժ�ͼӹ��е�һ�����ÿ��ÿ����Բ�ժ70���ӹ�35���谲��x�����˲�ժ��ݮ��ʣ�µĹ��˼ӹ���ݮ��
(1)������һ�������������ΪyԪ����y��x�ĺ�����ϵʽ��
![]() ������η��乤�ˣ�����ʹһ��������������������ֵ��
������η��乤�ˣ�����ʹһ��������������������ֵ��
���𰸡���1��y=-350x+63000����2������7�����˽��в�ժ��13�����˽��мӹ�������ʹһ�����������������Ϊ60550Ԫ��
��������
��1������������������=�������������������ɵó��𰸣�
��2���ɲ�ժ����ݮ����Ҫ���ڼӹ�����ݮ�����ó�x��ȡֵ��Χ���ٽ����1���������y��x�ĺ�����ϵʽ�����ɵó���.
�⣺��1����������ã�y=[70x-(20-x)��35]��40+(20-x)��35��130=-350x+63000
��y��x�ĺ�����ϵʽΪy=-350x+63000.
��2����70x��35(20-x)
��![]()
��x����������x��20
��7��x��20
��y=-350x+63000��k=-350<0
��y��ֵ����x���������С
�൱x=7ʱ��yȡ���ֵ�����ֵΪ-350��7+63000=60550
�𣺰���7�����˽��в�ժ��13�����˽��мӹ�������ʹһ�����������������Ϊ60550Ԫ��

 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�����Ŀ��������ѧϰ��һ�κ�����ʱ���۵ľ���ͷ�������������⣺
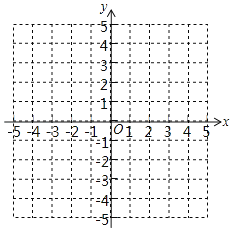
��1����ƽ��ֱ������ϵ�У���������y��|x|��ͼ��
���б���գ�
x | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� | �� �� | �� �� | �� �� | �� �� | �� �� | �� �� | �� �� | �� |
����㡢���ߣ�����y��|x|��ͼ��
��2�������������ͼ��д��y��|x|������ͬ���͵����ʣ�
��3�������������ͼ����|x|��2x��1��0�Ľ⣮