Question

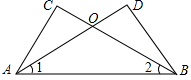如图，在△ABC和△ABD中，AD和BC交于点O，∠1=∠2，请你添加一个重要条件（不再添加其它线段，不再标注或使用其它字母），使AC=BD，并给出证明．你添加的条件是

∠C=∠D

．

Answer 1

分析：添加的条件是∠C=∠D，根据AAS推出△ABC≌△DAB，根据全等三角形的性质推出即可．

解答：添加的条件是∠C=∠D，
证明：∵在△ABC和△DAB中

∠C=∠D ∠2=∠1 AB=BA

，
∴△ABC≌△DAB（AAS），
∴AC=BD，
故答案为：∠C=∠D

点评：本题考查了全等三角形的性质和判定，注意：全等三角形的对应边相等，全等三角形的判定定理有SAS，ASA，AAS，SSS，答案不唯一．