Question

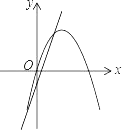
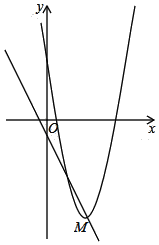
【题目】如图抛物线y＝ax2+2交x轴于点A（﹣2，0）、B，交y轴于点C；

（1）求抛物线的解析式；

（2）点P从点A出发，以1个单位/秒的速度向终点B运动，同时点Q从点C出发，以相同的速度沿y轴正方向向上运动，运动的时间为t秒，当点P到达点B时，点Q也停止运动，设△PQC的面积为S，求S与t间的函数关系式并直接写出t的取值范围；

（3）在（2）的条件下，当点P在线段OB上时，设PQ交直线AC于点G，过P作PE⊥AC于点E，求EG的长．

Answer 1

【答案】（1）y＝﹣x2+2；（2）S＝﹣t2+t（0＜t＜2）；S═t2﹣t（2＜t≤4）；（3）.

【解析】

（1）把A点坐标代入二次函数，解得a=-，即可求解；
（2）利用S=CQOP，分0＜t＜2、2＜t≤4两种情况求解即可；
（3）过点G作GH⊥y轴，利用HG∥OP，得=，求出GH=，利用GE=EC+CG=即可求解．

解：（1）把A点坐标代入二次函数，解得a＝﹣，

故：二次函数的表达式为：y＝﹣x2+2；

（2）S＝CQOP，

当0＜t＜2时，

S＝t（﹣t+2）＝﹣t2+t，

当2＜t≤4时，

S═t（t﹣2）＝t2﹣t；

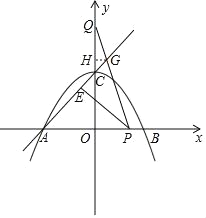
（3）t秒时，AP＝t，OP＝t﹣2，CQ＝t，

直线AC与x轴的夹角为45°，

则AE＝，GC＝GH，AC＝2，HC＝HG，

过点G作GH⊥y轴，交y轴于点H，

∵HG∥OP，

∴=，

即：= ，

解得：GH=，

则：GC＝GH＝

GE＝EC+CG＝AC﹣AE+GC＝2﹣+＝．