题目内容
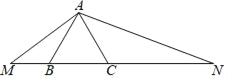
【题目】将边长为4的等边△ABC的边BC向两端延长,使∠MAN=120°.
(1)求证:△MAB∽△ANC;
(2)若CN=4MB,求线段CN的长.
【答案】(1)见解析;(2) CN=8
【解析】
(1)依据∠AMB+∠ANC=60°,∠AMB+∠MAB=∠ABC=60°,可得∠MAB=∠ANC,∠AMB=∠NAC,即可得到△MAB∽△ANC;
(2)由(1)得![]() ,再根据AB=BC=AC=4,CN=4MB,即可得到
,再根据AB=BC=AC=4,CN=4MB,即可得到![]() ,进而得出MB=2,CN=8.
,进而得出MB=2,CN=8.
解:(1)∵∠M+∠MAN+∠N=180°,∠MAN=120°,
∴∠AMB+∠ANC=60°,
又∵∠AMB+∠MAB=∠ABC=60°,
∴∠MAB=∠ANC,
同理∠AMB=∠NAC,
∴△MAB∽△ANC;
(2)由(1)得![]() ,
,
∵AB=BC=AC=4,CN=4MB,
∴![]() ,
,
∴MB=2,
∴CN=8.

练习册系列答案
相关题目