题目内容
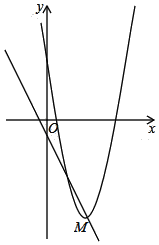
【题目】在平面直角坐标系中,抛物线![]() 的顶点M在直线L:
的顶点M在直线L:![]() 上.
上.
![]() 求直线L的函数表达式;
求直线L的函数表达式;
![]() 现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当
现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当![]() 时,求平移后的抛物线的解析式.
时,求平移后的抛物线的解析式.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
![]() 由题目已给出的抛物线一般式
由题目已给出的抛物线一般式![]() 直接化为顶点式
直接化为顶点式![]() 即可读出顶点坐标
即可读出顶点坐标![]() ,把顶点坐标代入直线L的解析式即可求出斜率
,把顶点坐标代入直线L的解析式即可求出斜率![]() ,进而写出直线L的解析式;
,进而写出直线L的解析式;
![]() 在直线L上取一点N,过N作
在直线L上取一点N,过N作![]() 轴于点E,构造
轴于点E,构造![]() 即
即![]() ,使得
,使得![]() ,则
,则![]() ,设平移后的二次函数的顶点式为
,设平移后的二次函数的顶点式为![]() ,则N点坐标为
,则N点坐标为![]() ,由
,由![]() 得,
得,![]() ,则C点坐标可以表示为
,则C点坐标可以表示为![]() ,又由N在直线L上,所以将N
,又由N在直线L上,所以将N![]() 代入
代入![]() 得,
得,![]() ,即平移后二次函数的顶点式可以为
,即平移后二次函数的顶点式可以为![]() ,把
,把![]() 代入其中,即可求出h’=3或 h’=-1,因为当对称轴在y轴左侧时抛物线与x轴无交点,与题意有又交点C不相符,则h’=-1应舍去,进而求得
代入其中,即可求出h’=3或 h’=-1,因为当对称轴在y轴左侧时抛物线与x轴无交点,与题意有又交点C不相符,则h’=-1应舍去,进而求得![]() 将h’和k’代入平移后二次函数的顶点式,再化为一般式即可.
将h’和k’代入平移后二次函数的顶点式,再化为一般式即可.
解:![]() 抛物线
抛物线![]()
所以![]() ,
,![]()
![]() 点的坐标为
点的坐标为![]()
又![]() 在直线L上
在直线L上
![]() 把
把![]() 代入
代入![]() 中得,
中得,![]()
解得,![]()
![]() 直线L的解析式为,
直线L的解析式为,![]()
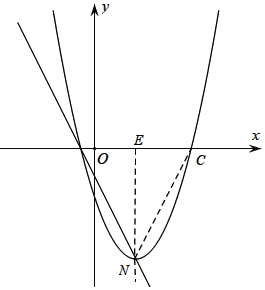
![]() 如图,设N(h′,k′),过N作
如图,设N(h′,k′),过N作![]() 轴于点E,连接NC.
轴于点E,连接NC.
由![]() 得,
得,![]() ,即
,即![]() .
.
![]() 点坐标为(h′-
点坐标为(h′-![]() k′,0)
k′,0)
又![]() 点N(h′,k′)在直线L上
点N(h′,k′)在直线L上
![]() 把N(h′,k′),代入
把N(h′,k′),代入![]() 得,k′=-2h′-2
得,k′=-2h′-2
设平移后的抛物线顶点式为y=![]() (x-h′)2+k′,
(x-h′)2+k′,
则把k′=-2h′-2代入上式得,y=![]() (x-h′)2-2h′-2
(x-h′)2-2h′-2
且h′-![]() k′=h′-
k′=h′-![]() (-2h′-2)=2h′+1
(-2h′-2)=2h′+1
∴C(2h′+1,0)
把C(2h′+1,0)代入y=![]() (x-h′)2-2h′-2得,
(x-h′)2-2h′-2得,
![]()
整理得,![]()
解得, h’=3或 h’=-1,
又![]() 当对称轴在y轴左边时抛物线与x轴无交点,这与题目已知条件“与x轴的右交点为C相矛盾
当对称轴在y轴左边时抛物线与x轴无交点,这与题目已知条件“与x轴的右交点为C相矛盾
∴h′=3,
k′=-2×3-2=-8
![]() 点坐标为
点坐标为![]()
![]() 平移后抛物线顶点式为,
平移后抛物线顶点式为,![]()
展开得,![]()

 考前必练系列答案
考前必练系列答案【题目】如图,已知![]() 是
是![]() (
(![]() )的函数,表1中给出了几组
)的函数,表1中给出了几组![]() 与
与![]() 的对应值:
的对应值:
表1:
| … |
| 1 |
| 2 |
| 3 | … |
| … | 6 | 3 | 2 |
|
| 1 | … |

(1)以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出![]() 的值;
的值;
(2)如果一次函数图像与(1)中图像交于![]() 和
和![]() 两点,在第一、四象限内当
两点,在第一、四象限内当![]() 在什么范围时,一次函数的值小于(1)中函数的值?请直接写出答案.
在什么范围时,一次函数的值小于(1)中函数的值?请直接写出答案.