题目内容
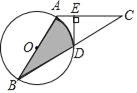
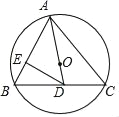
【题目】如图,已知锐角△ABC内接于⊙O,连接AO并延长交BC于点D.
(1)求证:∠ACB+∠BAD=90°;
(2)过点D作DE⊥AB于E,若∠ADC=2∠ACB,AC=4,求DE的长.
【答案】(1)见解析;(2)2.
【解析】
(1)如图1中,延长AD交⊙O于点F,连接BF.首先证明∠ABF=90°,再证明∠AFB=∠C即可解决问题.
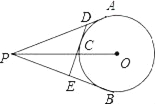
(2)如图2中,过点O作OH⊥AC于H,连接BO.想办法证明△BDE≌△AOH即可解决问题.
(1)证明:延长AD交⊙O于点F,连接BF.

∵AF为⊙O的直径,
∴∠ABF=90°,
∴∠AFB+∠BAD=90°,
∵∠AFB=∠ACB,
∴∠ACB+∠BAD=90°.
(2)证明:如图2中,过点O作OH⊥AC于H,连接BO.
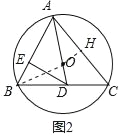
∵∠AOB=2∠ACB,
∠ADC=2∠ACB,
∴∠AOB=∠ADC,
∴∠BOD=∠BDO,
∴BD=BO,
∴BD=OA,
∵∠BED=∠AHO,∠ABD=∠AOH,
∴△BDE≌△AOH,(AAS),
∴DE=AH,
∵OH⊥AC,
∴AH=CH=![]() AC,
AC,
∴AC=2DE=4,
∴DE=2.

练习册系列答案
相关题目