题目内容
【题目】如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AECD=ADCE. 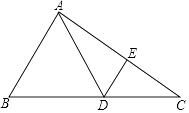
(1)求证:DE∥AB;
(2)如果点F是DE延长线上一点,且BD是DF和AB的比例中项,联结AF.求证:DF=AF.
【答案】
(1)证明:∵AECD=ADCE,
∴ ![]() ,
,
∵∠DAB=∠B,
∴AD=BD,
∴ ![]() ,
,
∴DE∥AB;
(2)证明:∵BD是DF和AB的比例中项,
∴BD2=DFAB,
∵AD=BD,
∴AD2=DFAB,
∴ ![]() ,
,
∵DE∥AB,
∴∠ADF=∠BAD,
∴△ADF∽△DBA,
∴ ![]() =1,
=1,
∴DF=AF.
【解析】(1)根据已知条件得到 ![]() ,根据等腰三角形的判定定理得到AD=BD,等量代换即可得到结论;(2)由BD是DF和AB的比例中项,得到BD2=DFAB,等量代换得到AD2=DFAB,推出
,根据等腰三角形的判定定理得到AD=BD,等量代换即可得到结论;(2)由BD是DF和AB的比例中项,得到BD2=DFAB,等量代换得到AD2=DFAB,推出 ![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到 ![]() =1,于是得到结论.
=1,于是得到结论.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

练习册系列答案
相关题目