题目内容
【题目】在4件同型号的产品中，有1件不合格品和3件合格品．
（1）从这4件产品中随机抽取1件进行检测，不放回，再随机抽取1件进行检测．请用列表法或画树状图的方法，求两次抽到的都是合格品的概率．（解答时可用A表示1件不合格品，用B、C．D分别表示3件合格品）
（2）在这4件产品中加入若干件合格品后，进行如下试验：随机抽取1件进行检侧，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，则可以推算出大约加入多少件合格品？
【答案】（1）
；（2） 16
【解析】
（1）利用树状图表示出所有可能出现的情况，找出抽到的都是合格品的情况，结合概率公式求解即可；
（2）设加入x件合格品，根据频率估计出抽到合格品的概率，再利用概率公式列出关于x的方程，解方程求得x的值.
（1）画出树状图.
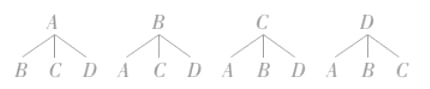
由树状图可知，共有12种等可能的情况，抽到的都是合格品的情况有6种，
由此可得P(抽到的都是合格品)=
=.
（2）设加入x件合格品，
∵大量重复试验后发现，抽到合格品的频率稳定在0.95，
∴抽到合格品的概率等于0.95，
根据题意得
=0.95，解得x=16.
经检验，x=16是原分式方程的根.
答：大约加入16件合格品.
练习册系列答案
相关题目
