��Ŀ����
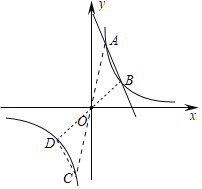
����Ŀ����ֱ֪��y��mx+n��m��0����m��nΪ��������˫����y��![]() ��k��0���ڵ�һ������A��B���㣬C��D�Ǹ�˫������һ֧�����㣬��A��B��C��D�ĵ㰴˳ʱ��˳�����У�
��k��0���ڵ�һ������A��B���㣬C��D�Ǹ�˫������һ֧�����㣬��A��B��C��D�ĵ㰴˳ʱ��˳�����У�
��1����ͼ����m����![]() ��n��
��n��![]() ����B��������Ϊ
����B��������Ϊ![]() ��
��
����k��ֵ��
�����߶�CD��ʹCD��AB��CD��AB��������������
��2�����ı���ABCDΪ���Σ�A������Ϊ��1��5����
����m��n��ֵ��
�ڵ�P��a��b����˫����y��![]() ��һ������һ���㣬��S��APC��24ʱ����a��ȡֵ��Χ���� ����
��һ������һ���㣬��S��APC��24ʱ����a��ȡֵ��Χ���� ����

���𰸡���1����k= 5���ڼ��������ɴ�AO��˫�����ڵ�C���ӳ�BO��˫�����ڵ�D���߶�CD��Ϊ����2����![]() ����0��a��1��a��5
����0��a��1��a��5
��������
��1�������ֱ�ߵĽ���ʽ�����ô���ϵ�������ɽ�����⣻����ͼ���ɴ�AO��˫�����ڵ�C���ӳ�BO��˫�����ڵ�D���߶�CD��Ϊ����
��2�������A��B�������꣬���ô���ϵ�������ɽ�����⣻�ڷ��������������PAC�������24ʱa��ֵ�������жϣ�
��1���١�![]() ��
��![]() ��
��
��ֱ�ߵĽ���ʽΪ![]() ��
��
�ߵ�B��ֱ���ϣ�������Ϊ![]() ��
��
��![]() ��
��
���x��2
��![]() ��
��
��![]() ��
��
������ͼ���ɴ�AO��˫�����ڵ�C���ӳ�BO��˫�����ڵ�D���߶�CD��Ϊ����
��2���١ߵ�![]() ��
��![]() �ϣ�
�ϣ�
��k��5��
���ı���ABCD�Ǿ��Σ�
��OA��OB��OC��OD��
��A��B����ֱ��y��x�Գƣ�
��![]() ��
��
����![]() �����
�����![]() ��
��
������ͼ������P�ڵ�A���Ҳ�ʱ������C����y��ĶԳƵ�C�䣬����AC��AC�䣬PC��PC�䣬PA��
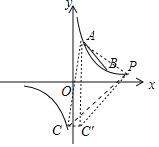
��A��C����ԭ��Գƣ�![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ʱ��
ʱ��
��![]() ��
��
��![]() ��
��
��a��5��![]() (����)��
(����)��
����P�ڵ�A�����ʱ��ͬ���ɵ�a��1��
������������a�ķ�ΧΪ![]() ��
��![]() ��
��