题目内容
【题目】如图,等边△ABC放置在平面直角坐标系中,已知A(0,0)、B(2,0),反比例函数的图象经过点C.
(1)求点C的坐标及反比例函数的解析式.
(2)如果将等边△ABC向上平移n个单位长度,使点B恰好落在双曲线上,求n的值.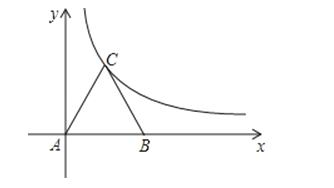
【答案】解:(1)过点C作CD⊥x轴,垂足为D,如图,设反比例函数的解析式为![]() ,
,
∵A(0,0)、B(2,0),
∴AB=2,
∵△ABC是等边三角形,
∴AC=AB=2,∠CAB=60°,
∴AD=1,CD=ACsin60=2×![]() =
=![]() ,
,
∴点C坐标为(1,![]() ),
),
∵反比例函数的图象经过点C,
∴k=1×![]() =
=![]() ,
,
∴反比例函数的解析式![]() ;
;
(2)∵将等边△ABC向上平移n个单位,则平移后B点坐标为(2,n),而平移后的点B恰好落在双曲线上,
∴2n=![]() ,
,
∴n=![]() .
.
【解析】(1)过点C作CD⊥x轴,垂足为D,如图,根据等边三角形的性质得到AC=AB=2,∠CAB=60°,AD=1,再利用三角函数可计算出CD![]() =
=![]() , 则点C坐标为(1,
, 则点C坐标为(1,![]() ),然后利用待定系数法求反比例函数解析式;
),然后利用待定系数法求反比例函数解析式;
(2)根据点平移规律得到平移后B点坐标为(2,n),然后根据反比例函数图象上点的坐标特征得到2n=![]() , 再解方程即可.
, 再解方程即可.
【考点精析】利用反比例函数的性质对题目进行判断即可得到答案,需要熟知性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某商场试销一种成本为每件120元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量![]() (件)是销售单价
(件)是销售单价![]() (元)的函数,并且满足如下对应值表:
(元)的函数,并且满足如下对应值表:
销售单价 | 130 | 140 | 145 |
销售量 | 110 | 100 | 95 |
(1)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(2)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于 2000元,试确定销售单价![]() 的范围.
的范围.