Question

【题目】如图，在每格为1个单位的正方形网格中建立直角坐标系，反比例函数y=的图象经过格点A．
（1）请写出点A的坐标、反比例函数y=的解析式；
（2）若点B（m，y1）、C（n，y2）（2＜m＜n）都在函数y=的图象上，试比较y1与y2的大小．

Answer 1

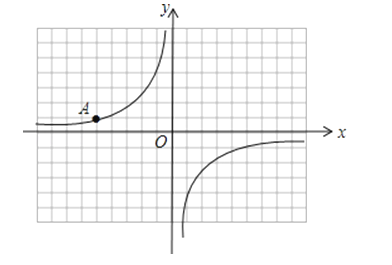
【答案】解：（1）由表得知A（﹣5，1），
∵反比例函数y=的图象经过格点A．
∴k=﹣5，
∴反比例函数y=的解析式为：y=﹣；
（2）∵k=﹣5＜0，
∴在每个象限内，y随x的增大而增大，
∵2＜m＜n，
∴y1＜y2 ．
【解析】（1）由图可得点A的坐标为：（﹣5，1），又由反比例函数y=经过A点，利用待定系数法即可求得反比例函数解析式；
（2）由反比例函数的性质：k＜0时，在每个象限内，y随x的增大而增大，因为2＜m＜n，所以B，C都在第四象限，所以y1＜y2 ．
【考点精析】本题主要考查了反比例函数的性质的相关知识点，需要掌握性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大才能正确解答此题．