题目内容
【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC. 

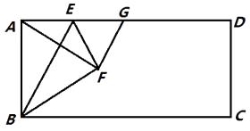
(1)如图1,若AB=3 ![]() ,BC=5,求AC的长;
,BC=5,求AC的长;
(2)如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
【答案】
(1)∵∠ABM=45°,AM⊥BM,
∴AM=BM=ABcos45°=3 ![]() ×
× ![]() =3,
=3,
则CM=BC﹣BM=5﹣2=2,
∴AC= ![]() =
= ![]() =
= ![]() ;
;
(2)延长EF到点G,使得FG=EF,连接BG.
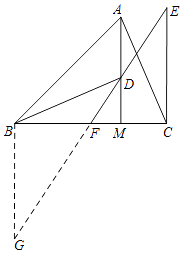
由DM=MC,∠BMD=∠AMC,BM=AM,
∴△BMD≌△AMC(SAS),
∴AC=BD,
又CE=AC,
因此BD=CE,
由BF=FC,∠BFG=∠EFC,FG=FE,
∴△BFG≌△CFE,
故BG=CE,∠G=∠E,
所以BD=BG=CE,
因此∠BDG=∠G=∠E.
【解析】(1)先由AM=BM=ABcos45°=3可得CM=2,再由勾股定理可得AC的长;(2)延长EF到点G,使得FG=EF,证△BMD≌△AMC得AC=BD,再证△BFG≌△CFE可得BG=CE,∠G=∠E,从而得BD=BG=CE,即可得∠BDG=∠G=∠E.
【考点精析】关于本题考查的勾股定理的概念,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.

练习册系列答案
相关题目