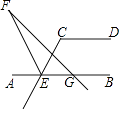题目内容
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.请解决下列问题: 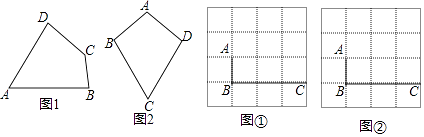
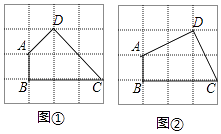
(1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=70°,∠B=75°,则∠C=°,∠D=°
(2)在探究等对角四边形性质时: 小红画了一个如图2所示的等对角四边形ABCD,其中,∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立,请你证明该结论;
(3)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个等对角四边形ABCD. 要求:四边形ABCD的顶点D在格点上,所画的两个四边形不全等.
(4)已知:在等对角四边形ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4,求对角线AC的长.
【答案】
(1)140;75
(2)证明:如图2,连接BD,
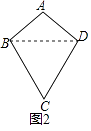
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ADC,
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB,
∴∠CBD=∠CDB,
∴CB=CD;
(3)如图所示:
(4)解:分两种情况:
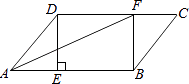
①当∠ADC=∠ABC=90°时,延长AD,BC相交于点E,如图3所示:
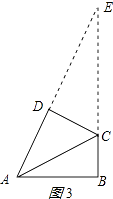
∵∠ABC=90°,∠DAB=60°,AB=5,
∴∠E=30°,
∴AE=2AB=10,
∴DE=AE﹣AD=10﹣4═6,
∵∠EDC=90°,∠E=30°,
∴CD=2 ![]() ,
,
∴AC= ![]() =
= ![]() =2
=2 ![]() ;
;
②当∠BCD=∠DAB=60°时,
过点D作DM⊥AB于点M,DN⊥BC于点N,如图4所示:
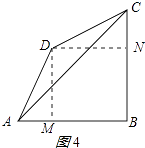
则∠AMD=90°,四边形BNDM是矩形,
∵∠DAB=60°,
∴∠ADM=30°,
∴AM= ![]() AD=2,
AD=2,
∴DM=2 ![]() ,
,
∴BM=AB﹣AM=5﹣2=3,
∵四边形BNDM是矩形,
∴DN=BM=3,BN=DM=2 ![]() ,
,
∵∠BCD=60°,
∴CN= ![]() ,
,
∴BC=CN+BN=3 ![]() ,
,
∴AC= ![]() =2
=2 ![]() .
.
综上所述:AC的长为2 ![]() 或2
或2 ![]() .
.
故答案为:140,75.
【解析】(1)解:∵四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=75°, ∴∠D=∠B=75°,
∴∠C=360°﹣75°﹣75°﹣70°=140°;
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握勾股定理的逆定理(如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形)的相关知识才是答题的关键.