题目内容
【题目】如图,□ ABCD中,E是AD边上一点,AD=4![]() ,CD=3,ED=
,CD=3,ED=![]() ,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将
,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将 ![]() CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.
CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.

【答案】![]() ,3,
,3,![]()
【解析】过点B作BF⊥AD于点F,连接BE,根据平行四边形的性质及已知条件,可证得△BEF是等腰直角三角形,求出BF、BE、的长,再利用三角形的外角性质结合已知,证明∠2=∠1,∠EBP=∠C,利用相似三角形的判定,可证得△BPE∽△CQP,再分三种情况讨论:①当CQ=QP时,则BP=PE,可证得四边形BPEF是矩形,可求出BP的长;②当CP=CQ时,则BP=BE=3;③当CP=PQ时,则BE=PE=3,再根据△BPE是等腰直角三角形,利用勾股定理,可求出BP的长,从而可得出答案.
如图,过点B作BF⊥AD于点F,连接BE
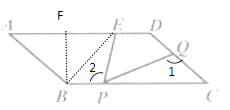
∵平行四边形ABCD
∴AD∥BC
∴∠BFE=∠FBP=90°
在Rt△ABF中,∠A=45°,AB=3
∴BF=AF=ABcos45°=3×![]() =
=![]()
∴EF=AD-AF-DE=4![]() -
-![]() -
-![]() =
=![]()
∴EF=BF
∴∠FBE=∠EBP=45°=∠C
∠2+∠EFQ=∠1+∠C
∵∠EFQ=∠C=45°
∴∠2=∠1
∴△BPE∽△CQP
将 △ CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,分三种情况:
①当CQ=QP时,则BP=PE
∴∠EBP=∠BEP=45°,则∠BPE=90°
∴四边形BPEF是矩形
∴BP=EF=![]()
②当CP=CQ时,则BP=BE=3
③当CP=PQ时,则BE=PE=3,∠BEP=90°
∴△BPE是等腰直角三角形
∴BP=![]() .
.
故答案为:![]() 、3、
、3、![]()

练习册系列答案
相关题目