Question

【题目】已知△ABC是等边三角形，点D是直线AB上一点，延长CB到点E，使BE＝AD，连接DE，DC，

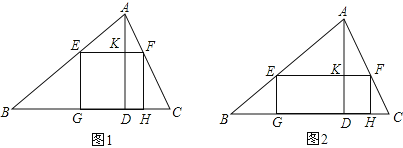
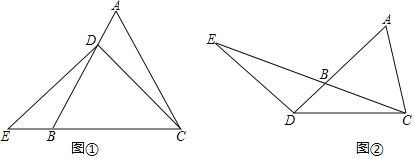
（1）若点D在线段AB上，且AB＝6，AD＝2（如图①），求证：DE＝DC；并求出此时CD的长；

（2）若点D在线段AB的延长线上，（如图②），此时是否仍有DE＝DC？请证明你的结论；

（3）在（2）的条件下，连接AE，若，求CD：AE的值．

Answer 1

【答案】（1）见解析，CD＝2；（2）DE＝DC，理由见解析；（3）CD：AE＝．

【解析】

（1）过点D作DF∥BC交AC于点F，作DM⊥BC于点M，由题意可证△ADF是等边三角形，可得AD=AF=DF=2=BE，可得∠DBE=∠DFC=120°，CF=DB=4，可证△DBE≌△CFD，可得DE=CD，由勾股定理可求CD的长；
（2）过点D作DF∥BC交AC的延长线于点F，由题意可证△ADF是等边三角形，可得AD=DF=AF，由“SAS”可证△EBD≌△DFC，可得DE=DC；
（3）过点C作CH⊥AB于点H，过点A作AN⊥BC于点N，设AB=2x，AD=3x，由等边三角形的性质可得BC=AC=2x，DF=BE=3x，BD=AD-AB=x，BN=BH=x，AN=x=CH，由勾股定理可求CD，AE的长，即可求CD：AE的值．

解：（1）过点D作DF∥BC交AC于点F，作DM⊥BC于点M，

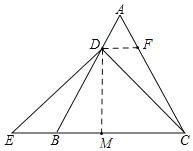
∵△ABC是等边三角形

∴∠ABC＝∠ACB＝∠A＝60°，AB＝AC＝BC＝6，

∴∠DBE＝120°

∵DF∥BC

∴∠ADF＝∠ABC＝60°，∠AFD＝∠ACB＝60°

∴△ADF是等边三角形，∠DFC＝120°

∴AD＝AF＝DF＝2，

∴BD＝AB﹣AD＝4＝AC﹣AF＝CF

∵BE＝AD＝DF＝2，∠DBE＝∠DFC＝120°，CF＝DB

∴△DBE≌△CFD（SAS）

∴DE＝DC

又∵DM⊥BC

∴CM＝EM＝EC＝（BE+BC）＝4

∵在Rt△DBM中，BD＝4，∠DBM＝60°

∴BM＝2，DM＝BM＝2

∴CD＝ ＝2 ；

（2）DE＝DC

理由如下：过点D作DF∥BC交AC的延长线于点F，

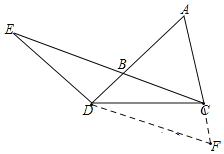
∵BC∥DF

∴∠ABC＝∠ADF＝60°，∠ACB＝∠AFD＝60°，

∴△ADF是等边三角形，

∴AD＝DF＝AF，

∴AD﹣AB＝AF﹣AC

∴BD＝CF，且BE＝AD＝DF，∠EBD＝∠ABC＝60°＝∠AFD

∴△EBD≌△DFC（SAS）

∴DE＝CD；

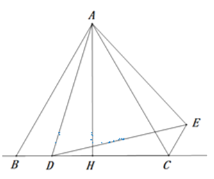
（3）如图，过点C作CH⊥AB于点H，过点A作AN⊥BC于点N，

∵

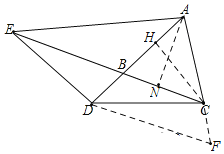
∴设AB＝2x，AD＝3x，

∴BC＝AC＝2x，DF＝BE＝3x，BD＝AD﹣AB＝x，

∵△ABC是等边三角形，AN⊥BC，CH⊥AB

∴BN＝BH＝x，AN＝ x＝CH

在Rt△DHC中，DC＝ ＝ x，

在Rt△AEN中，AE＝ ＝ x，

∴CD：AE＝ ＝ ．

故答案为：（1）见解析，CD＝2；（2）DE＝DC，理由见解析；（3）CD：AE＝．