题目内容
【题目】如图,在△ABC中,∠B=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线. 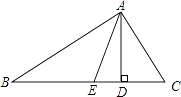
(1)求∠DAE的度数;
(2)写出以AD为高的所有三角形.
【答案】
(1)解:∵在△ABC中,AE是∠BAC的平分线,且∠B=40°,∠C=60°,
∴∠BAE=∠EAC= ![]() (180°﹣∠B﹣∠C)=
(180°﹣∠B﹣∠C)= ![]() (180°﹣40°﹣60°)=40°.
(180°﹣40°﹣60°)=40°.
在△ACD中,∠ADC=90°,∠C=60°,
∴∠DAC=180°﹣90°﹣60°=30°,
∠EAD=∠EAC﹣∠DAC=40°﹣30°=10°
(2)解:以AD为高的所有三角形:△ABC、△ABD、△ACE、△ABE、△ADF和△ACD
【解析】(1)根据三角形的内角和定理及角平分线的性质求解即可;(2)以AD为高的所有三角形是在BC线段上任意两点和点A组成的所有三角形.
【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内,以及对三角形的内角和外角的理解,了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
相关题目

