题目内容
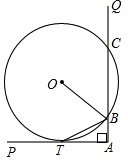
如图，∠PAQ是直角，半径为5的⊙O与AP相切于点T，与AQ相交于两点B、C．
（1）BT是否平分∠OBA？证明你的结论；
（2）若已知AT=4，试求AB的长．
（1）BT是否平分∠OBA？证明你的结论；
（2）若已知AT=4，试求AB的长．
（1）BT平分∠OBA，
证明：连接OT，
∵AT是切线，
∴OT⊥AP；
又∵∠PAB是直角，即AQ⊥AP，
∴AB∥OT，
∴∠TBA=∠BTO．
又∵OT=OB，
∴∠OTB=∠OBT．
∴∠OBT=∠TBA，即BT平分∠OBA；
（2）过点B作BH⊥OT于点H，则四边形OMBH和四边形ABHT都是矩形．
则在Rt△OBH中，OB=5，BH=AT=4，
∴OH=
=
=3，
∴AB=HT=OT-OH=5-3=2．
证明：连接OT，
∵AT是切线，
∴OT⊥AP；
又∵∠PAB是直角，即AQ⊥AP，
∴AB∥OT，
∴∠TBA=∠BTO．
又∵OT=OB，
∴∠OTB=∠OBT．
∴∠OBT=∠TBA，即BT平分∠OBA；
（2）过点B作BH⊥OT于点H，则四边形OMBH和四边形ABHT都是矩形．
则在Rt△OBH中，OB=5，BH=AT=4，
∴OH=
| OB2-BH2 |
| 52-42 |
∴AB=HT=OT-OH=5-3=2．
练习册系列答案
阅读快车系列答案
相关题目
