题目内容
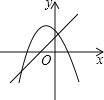
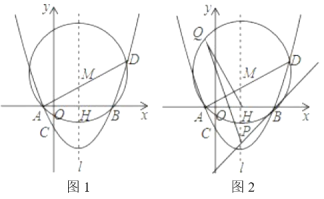
【题目】如图,![]() 的边
的边![]() 与经过
与经过![]() 三点的
三点的![]() 相切.
相切.
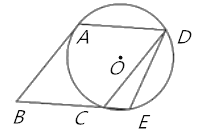
(1)求证:弧![]() 弧
弧![]() ;
;
(2)如图2,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 若
若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接AO并延长交DC于F.只要证明AF⊥DC,利用垂径定理即可解决问题;
(2)作出如图的辅助线,证得四边形ACED是等腰梯形结合(1)的结论得到AC=AD=DE,CM=EN,AM=DN,CE=MN,根据![]() ,设DE=
,设DE=![]() ,则EN=
,则EN=![]() ,DN
,DN![]() ,通过计算即可求解.
,通过计算即可求解.
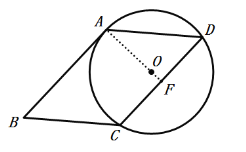
(1)连接AO并延长交BC于F.
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠FAB=∠DFA,
∵AB是⊙O的切线,
∴∠FAB =90°,
∴∠DFA =90°,
∴OF⊥DC,
∴A是![]() 的中点,
的中点,
∴![]() =
=![]() ;
;
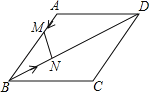
(2)如图,作CM⊥AD于M,EN⊥AD于N,连接AC.

由(1)得:A是![]() 的中点,
的中点,
∴AC=AD,
∵四边形ABCD是平行四边形,
∴![]() =
=![]() ,CE∥AD,
,CE∥AD,
∴AC=AD=DE,∠ADC=∠DCE,
∴四边形ACED是等腰梯形,
∴CM=EN,AM=DN,CE=MN,
∵![]() ,
,
设DE=![]() ,则EN=
,则EN=![]() ,DN=
,DN=![]() ,
,
∴CM=EN=![]() ,DM=AD-AM=DE-DN=
,DM=AD-AM=DE-DN=![]() ,
,
∴![]() .
.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】在“新冠病毒”防控期间,某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进同一商品的进价相同,具体情况如下表所示:
项目 | 购进数量(件) | 购进所需费用(元) | |
酒精消毒液 | 测温枪 | ||
第一次 | 30 | 40 | 8300 |
第二次 | 40 | 30 | 6400 |
(1)求酒精消毒液和测温枪两种商品每件的进价分别是多少元?
(2)公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于测温枪数量的4倍,求该公司销售完上述1000件商品获得的最大利润.