题目内容
【题目】在![]() 中,
中, ![]() ,点
,点![]() (不与点
(不与点![]() 重合)是线段
重合)是线段![]() 上的一个动点,连接
上的一个动点,连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作正方形
的右侧作正方形![]() ,连接
,连接![]()
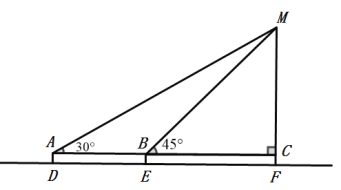
(1)发现问题:如图(1),若![]() ,则
,则![]() 与
与![]() 的位置关系_________;
的位置关系_________;
(2)拓展探究:如图(2),若![]() ,(1)中的结论是否仍然成立?请说明理由;
,(1)中的结论是否仍然成立?请说明理由;
(3)解决问题:若![]() ,设正方形
,设正方形![]() 的边
的边![]() 与线段
与线段![]() 相交于点
相交于点![]() ,请直接写出线段
,请直接写出线段![]() 的最大值
的最大值
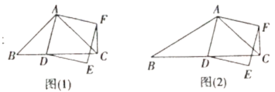
【答案】(1)![]() ;(2)仍然成立,见解析;(3)1
;(2)仍然成立,见解析;(3)1
【解析】
(1)由正切值可得∠ACB=45°,结合AB=AC,可知△ABC为等腰直角三角形,再利用正方形的性质可证明△BAD≌△CAF,进而得到∠ACF=45°,推出∠FCB=90°即可得证;
(2)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,同(1)可证CF⊥BD;
,同(1)可证CF⊥BD;
(3)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,易证
,易证![]() ,设
,设![]() 为
为![]() ,
,![]() 为
为![]() ,则
,则![]() ,根据对应边成比例建立y与x的函数关系,即可求出CP的最大值.
,根据对应边成比例建立y与x的函数关系,即可求出CP的最大值.
解:(1) ∵![]()
![]()
∵![]() ,
,
![]()
∴![]()
∵四边形![]() 是正方形,
是正方形,
∴![]()
∴![]() ,
,
∴![]() ,
,
在△BAD和△CAF中,
∵AB=AC,∠BAD=∠CAF,AD=AF
∴![]() (SAS),
(SAS),
∴![]() ,
,
∴![]() ,
,
即![]() .
.
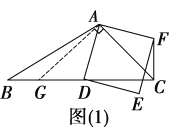
(2)(1)中的结论仍然成立,理由如下:
如图(1),过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
![]()
∴![]()
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在△GAD和△CAF中,
∵AG=AC,∠GAD=∠CAF,AD=AF
∴![]() (SAS),
(SAS),
∴![]() ,
,
∴![]() ,即
,即![]() .
.
∴(1)中的结论仍然成立.
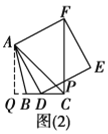
(3)线段![]() 的最大值为1.
的最大值为1.
如图(2),过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
∵![]()
∴![]() .
.
设![]() 为
为![]() ,
,![]() 为
为![]() ,则
,则![]() .
.
由(2)知, ![]() ,
,
∵∠ADE=90°
∴∠ADQ+∠CDP=90°
∵∠DPC+∠CDP=90°
∴∠ADQ=∠DPC
又∵∠AQD=∠DCP=90°,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴当![]() 时,
时, ![]() 有最大值1,
有最大值1,
即线段![]() 的最大值为1.
的最大值为1.

练习册系列答案
相关题目