题目内容
【题目】点![]() 在条直线上,点
在条直线上,点![]() 在
在![]() 轴上,若正方形
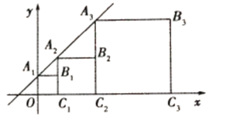
轴上,若正方形![]() 按如图所示的位置放置,且
按如图所示的位置放置,且![]() 的面积是1,直线
的面积是1,直线![]() 与
与![]() 轴的夹角是45°,则点
轴的夹角是45°,则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
首先求出直线![]() 解析式,然后依次找到A2,A3,A4的坐标,得出规律即可找到
解析式,然后依次找到A2,A3,A4的坐标,得出规律即可找到![]() 的坐标.
的坐标.
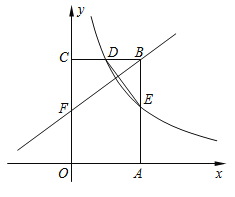
如图,设直线![]() 与x轴交于点B,
与x轴交于点B,

∵![]() 的面积是1
的面积是1
∴OA1=OC1=1,则A1坐标为(0,1)
∵∠A1BO=45°
∴△A1BO为等腰直角三角形,
∴OB= OA1=1,
则B点坐标为(-1,0),
设直线![]() 解析式
解析式![]() ,将A1,B的坐标代入得
,将A1,B的坐标代入得
![]() ,解得
,解得![]()
∴直线![]() 解析式为
解析式为![]()
∵OC1=1
∴A2的横坐标为1,
将x=1代入![]() ,得
,得![]() ,则A2的坐标为(1,2),
,则A2的坐标为(1,2),
∴A2C1=2= C1C2
则A3的横坐标为1+2=3,同理可得A3的坐标为(3,4),
∴A3C2=4= C2C3
则A4的横坐标为1+2+4=7,同理可得A4的坐标为(7,8),
以此类推,
An的横坐标为1+2+4+…+![]() =
=![]() ,An的坐标(
,An的坐标(![]() ,
,![]() ),
),
可得A2020的横坐标为![]() ,则A2020的坐标为(
,则A2020的坐标为(![]() ,
,![]() ),
),
故选C.

练习册系列答案
相关题目