题目内容
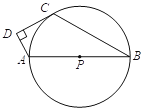
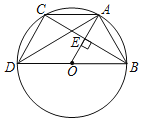
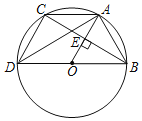
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,∠BAC=120°、OA⊥BC、若AB=4.
(1)求证:四边形OACD为菱形.
(2)求AD的长.
【答案】(1)证明见解析;(2)AD=4![]() .
.
【解析】
(1)由已知条件和垂径定理以及圆周角定理易证四边形OACD为平行四边形,再由邻边相等的平行四边形为菱形,可得结论;
(2)由(1)可知BD=2AB=8,在Rt△ABD中利用勾股定理即可求出AD的长.
(1)证明:∵OA⊥BC,
∴![]() ,
,
∴AB=AC,∠CDA=∠ADB=![]() ∠CDB,
∠CDB,
∵∠BAC=120°,
∴∠BDC=180°﹣120°=60°,
∴∠CDA=∠ADB=30°,
∵BD为⊙O的直径,
∴∠BAD=90°.
∴AC=AB=![]() BD,∠CAD=∠CAB﹣∠BAD=30°,
BD,∠CAD=∠CAB﹣∠BAD=30°,
∴AC∥OD,AC=OD,
∴四边形OACD为平行四边形,
又∵OA=OD,
∴四边形OACD为菱形;
(2)由(1)可知BD=2AB=8,
在Rt△ABD中,AD=![]() =4
=4![]() .
.

练习册系列答案
相关题目