Question

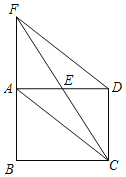
【题目】 如图，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点D是直线AB上一动点（不包含点A，B），过点B作BE⊥CD于点E，连接EA．

（1）如图1，当点D在线段AB上时，直接写出线段CE，BE，AE的数量关系：______．

（2）如图2，当点D在线段AB的延长线上时，判断线段CE，BE，AE的数量关系，并加以证明．

（3）如图3，当点D在线段BA的延长线上时，并将已知条件中的“AB=AC”改成；，其他条件不变，若CE=1，，请直接写出线段BE的长．

Answer 1

【答案】（1）；（2），证明见解析；（3）

【解析】

（1）作AF⊥AE交CE于F．证明△EAB≌△FAC（AAS），然后得出△AEF是等腰直角三角形，即可解决问题；

（2）作AH⊥CD于H，AG⊥EB于G．先证明∠AEB=∠AEC，根据角平分线的性质得出AG=AH，即可根据HL得出Rt△AGB≌Rt△AHC，然后得出△AEF是等腰直角三角形，从而可解决问题；

（3）作AF⊥AE交BE于F．先证明∠AEF=∠ACB=30°，有=，从而可得出△BAF∽△CAE，再利用相似三角形的性质以及勾股定理即可解决问题．

解：（1）结论：．

理由如下：如图1中，作AF⊥AE交CE于F．

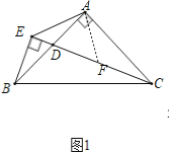
∵BE⊥EC，

∴∠BED=∠CAD=90°，

∵∠EDB=∠ADC，

∴∠EBD=∠ACD，

∵∠EAF=∠BAC=90°，

∴∠EAB=∠CAF，

∵AB=AC，

∴△EAB≌△FAC（AAS），

∴BE=CF，AE=AF，

∴△AEF是等腰直角三角形，

∴EF=AE，

∴EC-CF=EC-BE=EF=AE，

∴EC-BE=AE．

故答案为：EC-BE=AE．

（2）如图2中，结论：．

理由如下：作AH⊥CD于H，AG⊥EB于G．

∵∠BEC=∠BAC=90°，

∴∠BAC+∠CEB=180°，

∴A，B，E，C四点共圆，

∴∠AEC=∠ABC=45°，∠AEB=∠ACB=45°，

∴∠AEB=∠AEC，

∵AH⊥EC，AG⊥GE，

∴AG=AH，

∵AB=AC，∠AGB=∠AHC=90°，

∴Rt△AGB≌Rt△AHC（HL），

∴BG=CH，

∵∠AEH=∠EAH=∠AEG=∠EAG=45°，

∴AG=EG=AH=EH，∴AE=EH，

∴EC+EB=EH+CH+EG-GB=2EH=AE．

即BE+EC=AE．

（3）如图3中，作AF⊥AE交BE于F．

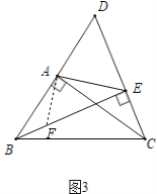
在Rt△ABC中，∵tan∠ABC==，

∴∠ABC=60°，∠ACB=30°，

∵∠BAC=∠BEC=90°，

∴A，B，C，E四点共圆，

∴∠AEF=∠ACB=30°，

∴AE=AF，

∴=，

∵∠BAC=∠EAF=90°，

∴∠BAF=∠CAE，

∴△BAF∽△CAE，

∴==，

∴BF=EC=，

∵AE=，

∴AF=1，

∴EF==2，

∴．