题目内容
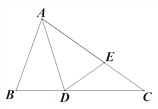
【题目】如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,E为AC上一点,AE=AB,连接DE.
(1)求证:△ABD≌△AED;
(2)已知BD=5,AB=9,求AC长.
【答案】(1)证明见解析; (2)AC=14
【解析】
试题(1)由AD是∠BAC的平分线,得出∠BAD=∠DAC,根据已知条件可证△ABD≌△AED;
(2)由△ABD≌△AED 得BD=DE,∠B=∠AED,再利用三角形外角的性质求证CE=DE,然后问题可解.
试题解析:(1)∵∠BAC的平分线AD交BC边于点D,
∴∠BAD=∠DAC,
在△ABD与△AED中,
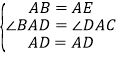 ,
,
∴△ABD≌△AED(SAS);
(2)∵△ABD≌△AED
∴BD=DE,∠B=∠AED,
∵∠B=2∠C,∠AED=∠C+∠EDC,
∴∠AED=2∠C,
∴∠C=∠EDC,
∴CE=DE,
∴CE=BD,
∴AC=AE+EC=AB+BD.
∵BD=5,AB=9
∴AC=14.

 阶梯计算系列答案
阶梯计算系列答案【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
【题目】为了传承优秀传统文化,我市组织了一次初三年级1 200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
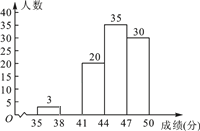
成绩分组 | 频数 | 频率(百分比) |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题:
(1)频率统计表中a=________,b=_______;
(2)请补全频数分布直方图;
(3)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?