题目内容
【题目】最近，“校园安全”受到全社会的广泛关注，重庆八中对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了如下两幅尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题：
（1）扇形统计图中“基本了解”部分所对应扇形的圆心角为度；请补全条形统计图；
（2）若达到“了解”程度的人中有1名男生2名女生，达到“不了解”的程度的人中有1名男生和1名女生，若分别从达到“了解”程度和“不了解”的人中分别抽取1人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1名男生和1名女生的概率．
【答案】
（1）120,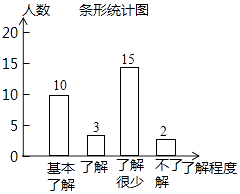
（2）解：设了解的学生为（A男，A女，A女），不了解的为（B男，B女），
则出现的所有可能性为：（A男，B男）、（A男、B女）、（A女，B男）、（A女，B女）、（A女，B男）、（A女，B女），
∴恰好抽到1名男生和1名女生的概率是：
，
即恰好抽到1名男生和1名女生的概率是 
．
【解析】解：（1）由题意可得，
本次调查的学生有：15÷50%=30（人），
扇形统计图中“基本了解”部分所对应扇形的圆心角为：360°× 
=120°，
了解的有：30﹣10﹣15﹣2=3（人），
（1）圆心角=360° 
百分比；条形统计图的补全关键是求出所缺部分的数量，部分
百分比=总数，具体量=样本容量 相应百分比；（2）
关注的结果为3个，机会均等所谓结果有6个，代入概率公式即可得概率为0.5.
练习册系列答案
相关题目
