Question

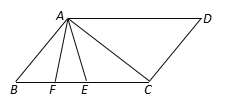
【题目】如图，AD∥BC，∠B＝∠D＝50°，点E、F在BC上，且满足∠CAD＝∠CAE，AF平分∠BAE．

（1）∠CAF＝ °；

（2）若平行移动CD，那么∠ACB与∠AEB度数的比值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值；

（3）在平行移动CD的过程中，是否存在某种情况，使∠AFB＝∠ACD？若存在，求出∠ACD度数；若不存在，说明理由．

Answer 1

【答案】（1）65°；（2）不变，1:2；（3）存在，97.5°

【解析】

（1）根据角平分线的性质可得∠CAF＝∠EAF+∠CAE=∠BAE+∠DAE=∠BAD，再根据平行线的性质得∠BAD =180-∠B，从而得出答案；

（2）根据平行线的性质得∠DAC=∠ACB，再由∠CAD＝∠CAE，可知∠ACB=∠CAE，从而可得∠AEB =2∠ACB，即可得出答案；

（3）根据平行线的性质得∠AFB=∠DAF=∠DAC+∠CAF，∠ACD=∠CAB=∠BAF+∠CAF，再由平行线的性质可得∠BAD=130°，即可求出答案

解：（1）∵AF平分∠BAE，

∴∠BAF=∠EAF=∠BAE，

∵∠CAD＝∠CAE

∴∠CAD＝∠CAE=∠DAE

∴∠CAF＝∠EAF+∠CAE=∠BAE+∠DAE=∠BAD

∵AD∥BC，∠B＝∠D＝50°，

∴∠BAD=180-∠B=130°,

∴∠CAF＝65°

（2）若平行移动CD，那么∠ACB与∠AEB度数的比值不发生变化.

∵AD∥BC，

∴∠DAC=∠ACB

∵∠CAD＝∠CAE

∴∠ACB=∠CAE

∴∠AEB=∠CAE+∠ACB=2∠ACB

即∠ACB：∠AEB=1:2

所以，∠ACB与∠AEB度数的比值是：1:2；

（3）存在

∵AD∥BC，

∴∠B+∠BAD=180°,

∵∠B=∠D

∴∠D+∠BAD=180°

∴AB∥CD

∴∠AFB=∠DAF=∠DAC+∠CAF

∠ACD=∠CAB=∠BAF+∠CAF

∵∠AFB＝∠ACD

∴∠DAC+∠CAF=∠BAF+∠CAF

∴∠DAC=∠BAF

∴∠DAC=∠BAF=∠CAE=∠EAF=∠BAD=×130°=32.5°

∴∠ACD= ∠CAB=∠BAF+∠CAF =3∠DAC=3×32.5°=97.5°