题目内容
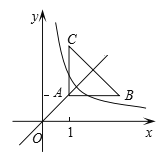
【题目】如图,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线![]() (k≠0)与△ABC有交点,则k的取值范围是( )
(k≠0)与△ABC有交点,则k的取值范围是( )
A. 1≤k≤4 B. 1≤k<4 C. 1<k<2 D. 1≤k≤3
【答案】A
【解析】分析:首先得出A、B、C三点的坐标,然后求出直线BC的解析式,然后根据反比例函数经过点A和反比例与一次函数只有一个交点分别求出k的值,从而得出k的取值范围.
详解:根据题意可得:A(1,1),B(3,1),C(1,3), ∴直线BC的解析式为y=-x+4,
当抛物线经过点A时,k=1,
当抛物线与直线BC有一个交点时,![]() ,即
,即![]() ,则△=16-4k=0,
,则△=16-4k=0,
解得:k=4, ∴k的取值范围为:1≤k≤4, 故选A.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】为拓展学生视野,促进书本知识与生活实践的深度融合,荆州市某中学组织八年级全体学生前往松滋洈水研学基地开展研学活动.在此次活动中,若每位老师带队14名学生,则还剩10名学生没老师带;若每位老师带队15名学生,就有一位老师少带6名学生,现有甲、乙两种大型客车,它们的载客量和租金如表所示:
甲型客车 | 乙型客车 | |
载客量(人/辆) | 35 | 30 |
租金(元/辆) | 400 | 320 |
学校计划此次研学活动的租金总费用不超过3000元,为安全起见,每辆客车上至少要有2名老师.
(1)参加此次研学活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆车上至少要有2名老师,可知租车总辆数为 辆;
(3)学校共有几种租车方案?最少租车费用是多少?