题目内容
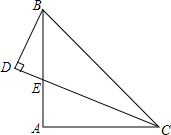 已知,如图△ABC中,AB=AC,∠A=90°,∠ACB的平分线CD交AB于点E,∠BDC=90°,求证:CE=2BD.
已知,如图△ABC中,AB=AC,∠A=90°,∠ACB的平分线CD交AB于点E,∠BDC=90°,求证:CE=2BD.考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:几何图形问题
分析:延长BD交CA的延长线于F,先证得△ACE≌△ABF,得出CE=BF;再证△CBD≌△CFD,得出BD=DF;由此得出结论即可.
解答:证明:如图,
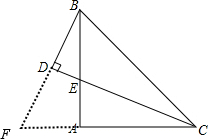
延长BD交CA的延长线于F,
∵∠BAC=90°
∴∠BAF=∠BAC=90°,∠ACE+∠AEC=90°,
∵∠BDC=90°
∴∠BDC=∠FDC=90°
∴∠ABF+∠BED=90°
∵∠AEC=∠BED
∴∠ACE=∠ABF
∵AB=AC
∴△ACE≌△ABF(ASA)
∴CE=BF
∵CD平分∠ACB
∴∠ACD=∠BCD
∵CD=CD
∴△CBD≌△CFD(ASA)
∴BD=FD=
BF
∴BD=
CE
∴CE=2BD.

延长BD交CA的延长线于F,
∵∠BAC=90°
∴∠BAF=∠BAC=90°,∠ACE+∠AEC=90°,
∵∠BDC=90°
∴∠BDC=∠FDC=90°
∴∠ABF+∠BED=90°
∵∠AEC=∠BED
∴∠ACE=∠ABF
∵AB=AC
∴△ACE≌△ABF(ASA)
∴CE=BF
∵CD平分∠ACB
∴∠ACD=∠BCD
∵CD=CD
∴△CBD≌△CFD(ASA)
∴BD=FD=
| 1 |
| 2 |
∴BD=
| 1 |
| 2 |
∴CE=2BD.
点评:此题考查三角形全等的判定与性质,角平分线的性质,根据已知条件,作出辅助线是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列调查中,适宜采用全面调查(普查)方式的是( )
| A、调查我市市民对“春运火车票抢票软件”的使用情况 |
| B、调查重庆中学生对“两会”的关注度 |
| C、调查人们在使用小米手机中容易出现的问题 |
| D、调查我校初三•一班学生本周三的睡眠时间 |
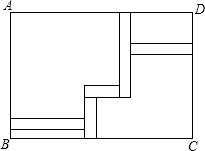 学校的课外生物小组的实验园地是一块长35米,宽26米的长方形,为了便于行走和管理,现要在中间修同样宽的到路,路宽均为a米,余下的作为种植面积,求种植面积是多少?
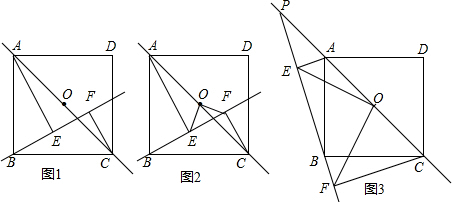
学校的课外生物小组的实验园地是一块长35米,宽26米的长方形,为了便于行走和管理,现要在中间修同样宽的到路,路宽均为a米,余下的作为种植面积,求种植面积是多少?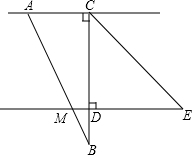 将一副直角三角板按图所示方式放置,∠ACB=∠CDE=90°,∠CAB=60°,∠ECD=45°,AB边交直线DE于点M,设∠BMD=α,∠BCE=β,将直角三角板ABC绕着点C旋转,在旋转过程中,点B始终位于直线DE下方,猜想变化过程中α与β的数量关系,并利用相交线与平行线的相关知识证明你的猜想.
将一副直角三角板按图所示方式放置,∠ACB=∠CDE=90°,∠CAB=60°,∠ECD=45°,AB边交直线DE于点M,设∠BMD=α,∠BCE=β,将直角三角板ABC绕着点C旋转,在旋转过程中,点B始终位于直线DE下方,猜想变化过程中α与β的数量关系,并利用相交线与平行线的相关知识证明你的猜想.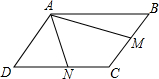 在平行四边形ABCD中,M,N分别是BC,DC的中点,AM=4,AN=3,且∠MAN=60°,求AB的长.
在平行四边形ABCD中,M,N分别是BC,DC的中点,AM=4,AN=3,且∠MAN=60°,求AB的长.