题目内容
已知正比例函数y=（m+2）x中，y的值随x的增大而增大，而正比例函数y=（2m-3）x，y的值随x的增大而减小，且m为整数，你能求出m的可能值吗？为什么？
考点：正比例函数的性质
专题：计算题
分析：先根据正比例函数y=（m+2）x中，y的值随x的增大而增大，得出m+2＞0，解得m＞-2．再由正比例函数y=（2m-3）x，y的值随x的增大而减小，得出2m-3＜0，解得m＜
．又m为整数，即可求出m的可能值．
| 3 |
| 2 |
解答：解：m的可能值为-1，0，1．理由如下：
∵正比例函数y=（m+2）x中，y的值随x的增大而增大，
∴m+2＞0，
解得m＞-2．
∵正比例函数y=（2m-3）x，y的值随x的增大而减小，
∴2m-3＜0，
解得m＜
．
∵m为整数，
∴m的可能值为-1，0，1．
∵正比例函数y=（m+2）x中，y的值随x的增大而增大，
∴m+2＞0，
解得m＞-2．
∵正比例函数y=（2m-3）x，y的值随x的增大而减小，
∴2m-3＜0，
解得m＜
| 3 |
| 2 |
∵m为整数，
∴m的可能值为-1，0，1．
点评：本题考查的是正比例函数的性质，熟知正比例函数y=kx（k≠0）中，当k＞0时，y随x的增大而增大；当k＜0时，y随x的增大而减小是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
学校的课外生物小组的实验园地是一块长35米，宽26米的长方形，为了便于行走和管理，现要在中间修同样宽的到路，路宽均为a米，余下的作为种植面积，求种植面积是多少？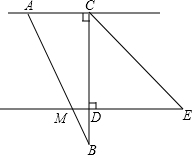
将一副直角三角板按图所示方式放置，∠ACB=∠CDE=90°，∠CAB=60°，∠ECD=45°，AB边交直线DE于点M，设∠BMD=α，∠BCE=β，将直角三角板ABC绕着点C旋转，在旋转过程中，点B始终位于直线DE下方，猜想变化过程中α与β的数量关系，并利用相交线与平行线的相关知识证明你的猜想．
在平行四边形ABCD中，M，N分别是BC，DC的中点，AM=4，AN=3，且∠MAN=60°，求AB的长．