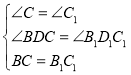题目内容
【题目】如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E. F,分别以E. F为圆心,以大于![]() EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
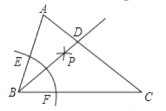
A.∠ADB=∠ABCB.AB=BDC.AC=AD+BDD.∠ABD=∠BCD
【答案】B
【解析】
根据作图方法可得BD平分∠ABC,进而可得∠ABD=∠DBC=![]() ∠ABC,然后根据条件∠ABC=2∠C可证明∠ABD=∠DBC=∠C,再根据三角形内角和外角的关系可得A说法正确;根据等角对等边可得DB=CD,进而可得AC=AD+BD,可得C说法正确;根据等量代换可得D正确.
∠ABC,然后根据条件∠ABC=2∠C可证明∠ABD=∠DBC=∠C,再根据三角形内角和外角的关系可得A说法正确;根据等角对等边可得DB=CD,进而可得AC=AD+BD,可得C说法正确;根据等量代换可得D正确.
由题意可得BD平分∠ABC,
A. ∵BD平分∠ABC,
∴∠ABD=∠DBC=![]() ∠ABC,
∠ABC,
∵∠ABC=2∠C,∠ADB=∠C+∠DBC,
∴∠ADB=2∠C,
∴∠ADB=∠ABC,故A不合题意;
B. ∵∠A≠∠ADB,
∴AB≠BD,故此选项符合题意;
C. ∵∠DBC=![]() ∠ABC,∠ABC=2∠C,
∠ABC,∠ABC=2∠C,
∴∠DBC=∠C,
∴DC=BD,
∵AC=AD+DC,
∴AC=AD+BD,故此选项不合题意;
D. ∵∠ABD=![]() ∠ABC,∠ABC=2∠C,
∠ABC,∠ABC=2∠C,
∴∠ABD=∠C,故此选项不合题意;
故选B.

练习册系列答案
相关题目