题目内容
如图,半径为2的⊙E交x轴于A、B,交y轴于点C、D,直线CF交x轴负半轴于点F,连接EB、EC.已知点E的坐标为(1,1),∠OFC=30°.
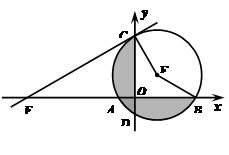
(1)求证:直线CF是⊙E的切线;(2)求证:AB=CD;(3)求图中阴影部分的面积.
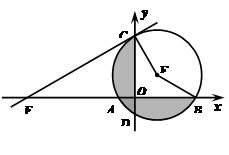
(1)求证:直线CF是⊙E的切线;(2)求证:AB=CD;(3)求图中阴影部分的面积.
(1)证明见解析;(2)证明见解析;(3)阴影部分的面积为( ).
).
 ).
).试题分析:(1)首先过点E作EG⊥y轴于点G,由点E的坐标为(1,1),可得EG=1.继而可求得∠ECG的度数,又由∠OFC=30°,∠FOC=90°,可求得∠FCE=∠OCF+∠ECG=90°.
(2)首先过点E作EH⊥x轴于点H,易证得Rt△CEG≌Rt△BEH,又由EH⊥AB,EG⊥CD,则可证得AB=CD;
(3)连接OE,可求得OC=
 +1与∠OEB+∠OEC=210°,继而可求得阴影部分的面积.
+1与∠OEB+∠OEC=210°,继而可求得阴影部分的面积.试题解析:(1)过点E作EG⊥y轴于点G,
∵点E的坐标为(1,1),
∴EG=1.
在Rt△CEG中,sin∠ECG=
 ,
,∴∠ECG=30°.
∵∠OFC=30°,∠FOC=90°,
∴∠OCF=180°﹣∠FOC﹣∠OFC=60°.
∴∠FCE=∠OCF+∠ECG=90°.
即CF⊥CE.
∴直线CF是⊙E的切线;
(2)过点E作EH⊥x轴于点H,
∵点E的坐标为(1,1),
∴EG=EH=1.
在Rt△CEG与Rt△BEH中,
∵
 ,
,∴Rt△CEG≌Rt△BEH(HL).
∴CG=BH.
∵EH⊥AB,EG⊥CD,
∴AB=2BH,CD=2CG.
∴AB=CD;
(3)连接OE,

在Rt△CEG中,CG=
 ,
,∴OC=
 +1.
+1.同理:OB=
 +1.
+1.∵OG=EG,∠OGE=90°,
∴∠EOG=∠OEG=45°.
又∵∠OCE=30°,
∴∠OEC=180°﹣∠EOG﹣∠OCE=105°.
同理:∠OEB=105°.
∴∠OEB+∠OEC=210°.
∴S阴影=
 .
.
练习册系列答案
相关题目
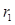 =2、
=2、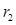 =4,若⊙O1与⊙O2的圆心距
=4,若⊙O1与⊙O2的圆心距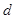 =5.则⊙O1与⊙O2的位置关系是___________.
=5.则⊙O1与⊙O2的位置关系是___________.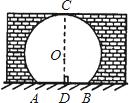
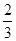 π cm2
π cm2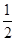 cm2 D.
cm2 D.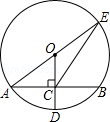
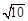 B. 2
B. 2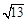 C. 2
C. 2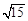 D. 8
D. 8 AD,则∠DBC的度数为
AD,则∠DBC的度数为 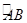 =
=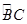 ,∠AOB=60°,则∠BDC的度数是( )
,∠AOB=60°,则∠BDC的度数是( )