题目内容
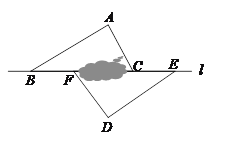
【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
【答案】(1)证明见解析(2)4cm
【解析】试题分析:(1)由平行线的性质得到∠ABC=∠DEF,再根据ASA证明△ABC≌△DEF即可;
(2)由全等三角形的性质得到BC=EF,从而有BF= EC,即可得到结论.
试题解析:(1)证明:∵AB∥DE,∴∠ABC=∠DEF.
在△ABC和△DEF中,∵∠ABC=∠DEF ,AB=DE,∠A=∠D,∴△ABC≌△DEF.
(2)解:∵△ABC≌△DEF,∴BC=EF,∴BF+FC=EC+FC,∴BF= EC.
∵BE=10cm,BF=3cm,∴FC=10-3-3=4cm.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某宾馆有50个房间共游客居住.当每个房间定价为180元时,房间会全部住满;当每个房间的定价增加10元时,就会有一个房间空闲.
设每个房间每天的定价增加x个10元.
(Ⅰ)填写下表:
每个房间每天定价(元) | 180 | 190 | 200 | 210 | …… | 180×10x |
住满房间个数(个) | 50 | 49 | 48 | …… |
(Ⅱ)若游客居住的房间的当天收入为y(元),写出y关于x的函数关系式;
(Ⅲ)如果游客入住房间,宾馆需对每个房间每天支出20元的各种费用.当房间定价为多少的时候,宾馆获得的利润W(元)最大?