题目内容
【题目】以下是推导“三角形内角和定理”的学习过程,请补全证明过程及推理依据.

已知:如图,△ABC.
求证:∠A+∠B+∠C=180°.
证明:过点A作DE∥BC,(请在图上画出该辅助线并标注D,E两个字母)
∠B=∠BAD,∠C= .( )
∵点D,A,E在同一条直线上,
∴ (平角的定义)
∴∠B+∠BAC+∠C=180°
即三角形的内角和为180°.
【答案】∠EAC;两直线平行,内错角相等;∠DAB+∠BAC+∠CAE=180°
【解析】
过点A作DE∥BC,依据平行线的性质,即可得到∠B=∠BAD,∠C=∠EAC,再根据平角的定义,即可得到三角形的内角和为180°.
证明:如图,过点A作DE∥BC,
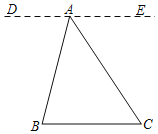
则∠B=∠BAD,∠C=∠EAC.( 两直线平行,内错角相等)
∵点D,A,E在同一条直线上,
∴∠DAB+∠BAC+∠CAE=180°(平角的定义)
∴∠B+∠BAC+∠C=180°
即三角形的内角和为180°.
故答案为:∠EAC;两直线平行,内错角相等;∠DAB+∠BAC+∠CAE=180°.

练习册系列答案
相关题目




