Question

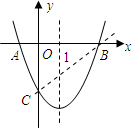
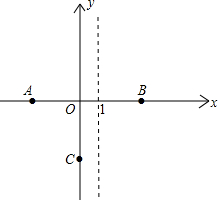
抛物线y₁=ax²+bx+c交x轴于A、B两点，交y轴于点C，对称轴为直线x=1，且A、C两点的坐标分别为A（-1，0）、C（0，-3）．
（1）求抛物线y₁=ax²+bx+c和直线BC：y₂=mx+n的解析式；
（2）当y₁•y₂≥0时，直接写出x的取值范围．

Answer 1

（1）∵抛物线y₁=ax²+bx+c的对称轴为x=1，且A点的坐标为A（-1，0），
∵A、B两点关于x=1对称，
∴B点坐标为（3，1），
∵抛物线y₁=ax²+bx+c经过A（-1，0）、B（3，0），C（0，-3），
∴

a-b+c=0 9a+3b+c=0 c=-3

，
解得a=1，b=-2，c=-3，
∴抛物线的解析式为y₁=x²-2x-3；
直线y₂=mx+n经过B（3，0），C（0，-3），
∴

0=3m+n n=-3

，
解得m=1，n=-3，
故直线解析式为y₂=x-3；

（2）连接BC，
若y₁•y₂≥0，
则抛物线y₁=ax²+bx+c和直线BC：y₂=mx+n图象在同一象限，
由图象可以看出当x＜-1时，y₁＞0，y₂＜0，
当x≥-1，y₁•y₂≥0，
即当y₁•y₂≥0时，x的取值范围为x≥-1．