题目内容
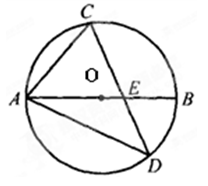
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=4cm,则CB的长为
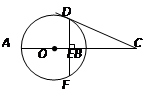
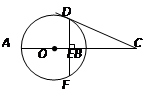
A.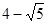 | B. | C.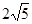 | D.4 |
B
连接OD.
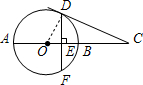
∵DF⊥AB,∴DE=DF=1.
根据勾股定理,得OD=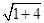 =
=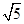 .
.
∵CD切⊙O于点D,
∴OD⊥CD,
∴△ODE∽△DCE,
∴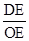 =
=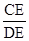 ,
,
即CE=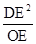 =4,
=4,
则BC=CE+0E-OB=5-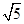 .
.
故选B.
此题综合运用了垂径定理、勾股定理、切线的性质、相似三角形的判定和性质.

∵DF⊥AB,∴DE=DF=1.
根据勾股定理,得OD=
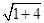 =
=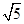 .
.∵CD切⊙O于点D,
∴OD⊥CD,
∴△ODE∽△DCE,
∴
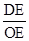 =
=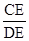 ,
,即CE=
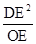 =4,
=4,则BC=CE+0E-OB=5-
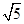 .
.故选B.
此题综合运用了垂径定理、勾股定理、切线的性质、相似三角形的判定和性质.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目

 宽为10米,净
宽为10米,净 为7米,则此隧道单心圆的半径
为7米,则此隧道单心圆的半径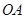 是( )
是( )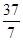
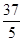
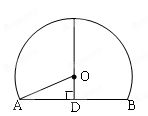
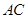 与
与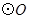 相切于点
相切于点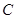 ,线段
,线段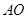 交
交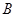 .过点
.过点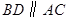 交
交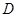 ,连接
,连接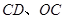 ,且
,且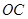 交
交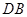 于点
于点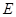 .若
.若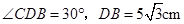 .
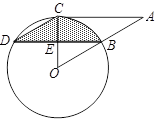
.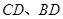 与弧
与弧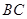 所围成的阴影部分的面积.(结果保留
所围成的阴影部分的面积.(结果保留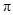 )
)
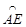 是劣弧
是劣弧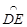 的2倍;⑤DE=DC。其中正确结论有( )
的2倍;⑤DE=DC。其中正确结论有( )
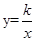 与⊙O的一个交点,图中阴影部分的面积为5π,则k的值为
与⊙O的一个交点,图中阴影部分的面积为5π,则k的值为