题目内容
已知,如图,P是正方形ABCD内一点,在正方形ABCD外有一个点E,满足∠ABE=∠CBP,BE=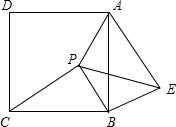 BP
BP(1)求证:△CPB≌△AEB;
(2)求证:PB⊥BE;
(3)若∠APB=135°,判断△PAE形状,并説明你的理由.
分析:(1)由四边形ABCD是正方形,可得AB=CD,根据全等三角形的判定定理即可证明;
(2)四边形ABCD是正方形,可得∠ABC=90°,即∠CBP+∠ABP=90°,又∠ABE=∠CBP,可得∠ABE+∠ABP=90°即可证明;
(3)求出∠PBE=90°,∵BE=BP,可得∠BPE=∠BEP=
(180°-∠PBE)=
×90°=45°,所以∠APE=∠APB-∠BPE=135°-45°=90°即可证明.
(2)四边形ABCD是正方形,可得∠ABC=90°,即∠CBP+∠ABP=90°,又∠ABE=∠CBP,可得∠ABE+∠ABP=90°即可证明;
(3)求出∠PBE=90°,∵BE=BP,可得∠BPE=∠BEP=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:∵四边形ABCD是正方形,
∴AB=CD,
又∵∠ABE=∠CBP,BE=BP,
∴△CPB≌△AEB(SAS);
(2)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,
即∠CBP+∠ABP=90°.
∵∠ABE=∠CBP,
∴∠ABE+∠ABP=90°,
即∠PBE=90°,
∴PB⊥BE;
(3)解:△PAE是直角三角形.
理由:由(2)知PB⊥BE,
∴∠PBE=90°.
∵BE=BP,
∴∠BPE=∠BEP=
(180°-∠PBE)=
×90°=45°,
∴∠APE=∠APB-∠BPE=135°-45°=90°,
∴△PAE是直角三角形.
∴AB=CD,
又∵∠ABE=∠CBP,BE=BP,
∴△CPB≌△AEB(SAS);
(2)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,
即∠CBP+∠ABP=90°.
∵∠ABE=∠CBP,
∴∠ABE+∠ABP=90°,
即∠PBE=90°,
∴PB⊥BE;
(3)解:△PAE是直角三角形.
理由:由(2)知PB⊥BE,
∴∠PBE=90°.
∵BE=BP,
∴∠BPE=∠BEP=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠APE=∠APB-∠BPE=135°-45°=90°,
∴△PAE是直角三角形.
点评:本题主要考查了正方形的性质和全等三角形的判定及性质,难度适中,关键是掌握正方形的性质和全等三角形的判定及性质的运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
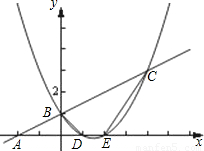
 4,6),且AB=
4,6),且AB=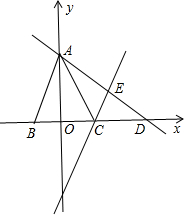 将△AOC沿直线AC折叠,点O落在平面内的点E处,直线AE交x轴于点D.
将△AOC沿直线AC折叠,点O落在平面内的点E处,直线AE交x轴于点D. 已知:如图,一次函数y=
已知:如图,一次函数y= 已知:如图所示,直线l的解析式为
已知:如图所示,直线l的解析式为 x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y= x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)