题目内容
28、已知：如图，在矩形ABCD中，E、F分别是边BC、AB上的点，且EF=ED，EF⊥ED．求证：AE平分∠BAD．
分析：要证AE平分∠BAD，可转化为△ABE为等腰直角三角形，得AB=BE，又AB=CD，再将它们分别转化为两全等三角形的两对应边，根据全等三角形的判定，和矩形的性质，可确定ASA．即求证．
解答：证明：∵四边形ABCD是矩形，
∴∠B=∠C=∠BAD=90°，AB=CD，（1分）
∴∠BEF+∠BFE=90°．
∵EF⊥ED，
∴∠BEF+∠CED=90°．（2分）
∴∠BFE=∠CED．
∴∠BEF=∠CDE．（3分）
又∵EF=ED，
∴△EBF≌△DCE．
∴BE=CD．（4分）
∴BE=AB．∴∠BAE=∠BEA=45°．（5分）
∴∠EAD=45°．
∴∠BAE=∠EAD．（6分）
∴AE平分∠BAD．（7分）
∴∠B=∠C=∠BAD=90°，AB=CD，（1分）
∴∠BEF+∠BFE=90°．
∵EF⊥ED，
∴∠BEF+∠CED=90°．（2分）
∴∠BFE=∠CED．
∴∠BEF=∠CDE．（3分）
又∵EF=ED，
∴△EBF≌△DCE．
∴BE=CD．（4分）
∴BE=AB．∴∠BAE=∠BEA=45°．（5分）
∴∠EAD=45°．
∴∠BAE=∠EAD．（6分）
∴AE平分∠BAD．（7分）
点评：三角形全等的判定是中考的热点．求证的结果可一步步转化为全等三角形的对应边、对应角相等．
练习册系列答案
天天向上口算本系列答案
相关题目
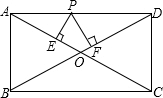已知，如图，在矩形ABCD中，P是边AD上的动点，PE垂直AC于E，PF垂直BD于F，如果AB=3，AD=4，那么（ ）A、PE+PF=
| ||||
B、
| ||||
| C、PE+PF=5 | ||||
| D、3＜PE+PF＜4 |
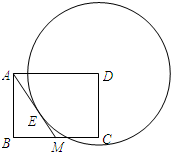已知，如图，在矩形ABCD中，M是边BC的中点，AB=3，BC=4，⊙D与直线AM相切于点E，
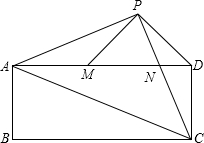已知：如图，在矩形ABCD中，AC是对角线．点P为矩形外一点且满足AP=PC，AP⊥PC．PC交AD于点N，连接DP，过点P作PM⊥PD交AD于M．
已知：如图，在矩形ABCD中，AB=4，AD=10，F是AD上一点，CF⊥EF于点F交AB于点E，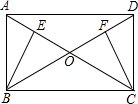
已知：如图，在矩形ABCD中，对角线AC与BD相交于点O，BE⊥AC于E，CF⊥BD于F，请你判断BE与CF的大小关系，并说明你的理由．