题目内容
【题目】已知二次函数y=x2+2x+
与x轴有两个交点，且k为正整数．
（1）求k的值；
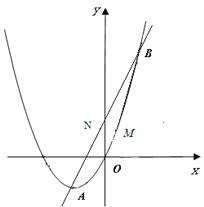
（2）当二次函数y=x2+2x+
图象经过原点时，直线y=3x+2与之交于A、B两点，若M是抛物线上在直线y=3x+2下方的一个动点，△MAB面积是否存在最大值？若存在，请求出M点坐标，并求出△MAB面积最大值；若不存在，请说明理由.
（3）将（2）中的二次函数图象x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分保持不变，翻折后的图象与原图象x轴上方的部分组成一个新图象.若直线y=kx+2（k>0）与该新图象恰好有三个公共点，求k的值．
【答案】（1）k为1，2；
（2）M坐标为
，S△MAB=
；
（3）k=1或
时，与该新图象恰好有三个公共点．
【解析】试题分析：（1）利用一元二次方程根的判别式可得到关于k的不等式，利用k为正整数可求得k的值；
（2）由条件可求得k的值，则可求得二次函数解析式，可求得A、B坐标，利用二次函数的性质可求得线段MN的最大值及此时点M的坐标；
（3）可画出二次函数的图象，当直线过A点时，可知直线与抛物线有三个公共点，当直线不过A点时，结合函数图象，利用方程可求得对应的b的值．
试题解析：（1）∵二次函数y=x2+2x+
与x轴有两个交点
∴Δ=
∴k﹣1＜2．
∴k＜3．
∵k为正整数，
∴k为1，2．
（2）把x=0代入方程x2+2x+
得k=1，
此时二次函数为y=x2+2x，
此时直线y=3x+2与二次函数y=x2+2x的交点为A（﹣1，-1），B（2，8）
设与直线y=3x+2平行的直线为y=3x+b，列方程组得： 
即：x2-x-b=0，△=b2-4ac=1+4b=0，所以b=
时有一个交点，代入求得交点M坐标为(
， 
).
过点M作MN∥x轴交直线AB于点N，点N坐标为(
， 
).
∴MN=
.
∴S△MAB=
MN(yB-yA)= 
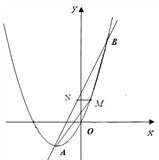
（3）由于新图象的封闭部分与原图象的封闭部分关于x轴对称，所以其解析式为y=﹣x2﹣2x，
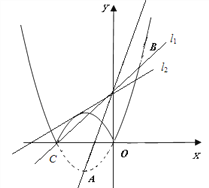
当直线与新图象有3个公共点（如图所示），直线为l1 、l2，其中l1 过点C，l2与翻转部分图象有一个交点.分为以下两种情况：
①直线l1：y=kx+2过点C（-2，0），代入y=kx+2得：k=1.
②直线l2：
则
有一组解，此时
有两个相等的实数根，
即△=0，解得： 
， 
（舍去）
综上所述k=1或
时，与该新图象恰好有三个公共点．
