Question

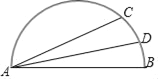
【题目】如图，在半圆O中，AB是直径，AB=13，点C是半圆O上一点，AC=12，弦AD平分∠BAC，则sin∠DAB=_____．

Answer 1

【答案】

【解析】

作辅助线，构建直角△ACF，先求BC和CE的长，利用平行相似证明△ACF∽△DEF，可得CF的长，从而计算AF的长，根据三角函数定义可得结论．

解：连接BC、OD，BC与OD交于点E，BC与AD交于F，

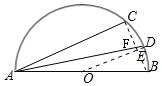
∵在半圆O中，AB是直径，

∴∠ACB=90°，∠CAB=2∠BAD，

∵AB=13，点C是半圆O上一点，AC=12，

∴BC=5，

∵弦AD平分∠BAC，

∴∠CAB=2∠BAD，

∵∠BOD=2∠BAD，

∴∠BAC=∠BOD，

∴AC∥OD，

∵AO=BO，

∴OE=AC=6，

∴∠OEB=∠ACB，

∴∠OEB=90°，

∴BE=CE=BC＝，

∵DE∥AC，

∴△ACF∽△DEF，

∴＝，

∵OE=6，OD=，

∴DE=，

∴＝=24，

∴CF=24EF，

∵CE=，

∴CF=CE=×=，

∴AF==，

∴sin∠DAF=sin∠CAF===．

故答案为：．