题目内容
【题目】如图，已知抛物线与x轴交于A（－1，0），B（3，0），与y轴交于C（0，－3），顶点为点M．
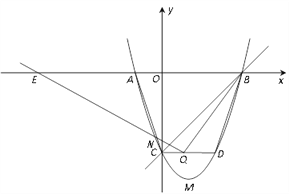
（1）求抛物线的解析式及点M的坐标．
（2）点P是直线BC在y轴右侧部分图象上的动点，若点P，点C，点M所构成的三角形与△AOC相似，求符合条件的P点坐标．
（3）过点C作CD∥AB，CD交抛物线于点D，点Q是线段CD上的一动点，作直线QN与线段AC交于点N，与x轴交于点E，且∠BQE＝∠BDC，当CN的值最大时，求点E的坐标．
【答案】 （1）y＝x2－2x－3,M（1，－4）;（2）P1（
，－
），P2（3，0）;（3）E（－10，0）．
【解析】试题分析：（1）由抛物线经过的三个已知点，可设抛物线的解析式为y＝a(x＋1)(x－3)，把C点坐标代入求a的值；（2）连接MC，作MF⊥y轴于点F，构造出直角三角形，由直角三角形相似，对应边成比例分情况讨论即可；（3）先求出点D的坐标，可求出线段BD的值，由抛物线的轴对称性可得到△NCQ∽△QDB，利用相似三角形对应边成比例即可求解．
试题解析：（1）∵抛物线与x轴交于A（－1，0），B（3，0），
∴设抛物线的解析式为y＝a(x＋1)(x－3)．
把（0，－3）代入y＝a(x＋1)(x－3)，解得a＝1．
∴抛物线的解析式为y＝x2－2x－3．
∵y＝x2－2x－3＝(x－1)2－4，
∴点M的坐标是（1，－4）．
（2）连接MC，作MF⊥y轴于点F，则点F坐标为（0，－4）．
∵MF＝1，CF＝－3－(－4)＝1，
∴MF＝CF，MC＝
．
∴∠FCM＝∠FMC＝45°．
∵B（3，0），C（0，－3），∴OB＝OC＝3．
而∠BOC＝90°，∴∠OCB＝∠OBC＝45°．
∴∠MCB＝180°－∠OCB－∠FCM＝90°．
由此可知，∠MCP＝90°，则点O与点C必为相似三角形对应点．
过点P作PH⊥y轴于H．
①若有△PCM∽△AOC，则有
＝
．
∴CP＝
＝
＝
．
∵∠PCH＝45°，CP＝，
∴PH＝CH＝÷＝．
∴OH＝OC－CH＝3－＝．
∴P1（，－）；
②若有△PCM∽△COA，则有
＝
．
∴CP＝
＝
＝
．
∴PH＝CH＝÷＝3．此时，点P与点B重合．
∴P2（3，0）．
∴符合题意的P点坐标为P1（，－），P2（3，0）．
（3）过点Q作QG⊥x轴于点G．
设点E的坐标为（n，0），Q的坐标为（m，－3）．
∵CD∥x轴，
∴D的纵坐标为－3．
把y＝－3代入y＝x2－2x－3，
∴x＝0或x＝2．
∴D（2，－3）．
∵B（3，0），
∴由勾股定理可求得：BD＝
．
∵Q（m，－3），
∴QD＝2－m，CQ＝m（0≤m≤2）．
∵∠BQE＝∠BDC，∠EQC＋∠BQE＝∠BDC＋∠QBD，
∴∠EQC＝∠QBD．
又由抛物线的轴对称性可知：∠NCQ＝∠BDC，
∴△NCQ∽△QDB．
∴
＝
．
∴
＝
．
∴CN＝－
(m2－2m)＝－(m－1)2＋．
∴当m＝1时，CN可取得最大值．此时Q的坐标为（1，－3）．
∴QG＝3，BG＝2，QD＝1．
∴由勾股定理可求得：QB＝
．
∵E（n，0），
∴EB＝3－n．
∵CD∥x轴，
∴∠BEQ＝∠NQC＝∠QBD，∠EBQ＝∠BQD．
∴△EQB∽△BDQ．
∴
＝
．
∴BQ2＝QDEB，即13＝1×(3－n)，
∴n＝－10．
∴E的坐标为（－10，0）．
