题目内容
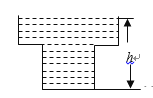
【题目】如图1，地面BD上两根等长立柱AB，CD之间悬挂一根近似成抛物线y=
x2﹣
x+3的绳子．
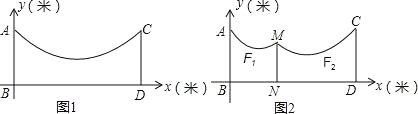
（1）求绳子最低点离地面的距离；
（2）因实际需要，在离AB为3米的位置处用一根立柱MN撑起绳子（如图2），使左边抛物线F1的最低点距MN为1米，离地面1.8米，求MN的长；
（3）将立柱MN的长度提升为3米，通过调整MN的位置，使抛物线F2对应函数的二次项系数始终为
，设MN离AB的距离为m，抛物线F2的顶点离地面距离为k，当2≤k≤2.5时，求m的取值范围．
【答案】（1）
m；（2）MN的长度为2.1m；（3）m的取值范围是4≤m≤8﹣2
．
【解析】
试题分析：（1）直接利用配方法求出二次函数最值得出答案；（2）利用顶点式求出抛物线F1的解析式，进而得出x=3时，y的值，进而得出MN的长；（3）根据题意得出抛物线F2的解析式，得出k的值，进而得出m的取值范围．
试题解析：（1）∵a=
＞0，
∴抛物线顶点为最低点，
∵y=x2﹣
x+3=（x﹣4）2+
，
∴绳子最低点离地面的距离为：
m；
（2）由（1）可知，对称轴为x=4，则BD=8，
令x=0得y=3，
∴A（0，3），C（8，3），
由题意可得：抛物线F1的顶点坐标为：（2，1.8），
设F1的解析式为：y=a（x﹣2）2+1.8，
将（0，3）代入得：4a+1.8=3，
解得：a=0.3，
∴抛物线F1为：y=0.3（x﹣2）2+1.8，
当x=3时，y=0.3×1+1.8=2.1，
∴MN的长度为：2.1m；
（3）∵MN=DC=3，
∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上，
∴抛物线F2的顶点坐标为：（
m+4，k），
∴抛物线F2的解析式为：y=
（x﹣m﹣4）2+k，
把C（8，3）代入得：（8﹣m﹣4）2+k=3，
解得：k=﹣（4﹣m）2+3，
∴k=﹣
（m﹣8）2+3，
∴k是关于m的二次函数，
又∵由已知m＜8，在对称轴的左侧，
∴k随m的增大而增大，
∴当k=2时，﹣（m﹣8）2+3=2，
解得：m1=4，m2=12（不符合题意，舍去），
当k=2.5时，﹣（m﹣8）2+3=2.5，
解得：m1=8﹣2 ，m2=8+2（不符合题意，舍去），
∴m的取值范围是：4≤m≤8﹣2．
