题目内容
如图，将矩形纸片ABCD沿AE向上折叠，使点B落在DC边上的F点处．若△AFD的周长为9，△ECF的周长为3，则矩形ABCD的周长为 ．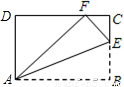
【答案】分析：折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
解答：解：由折叠的性质知，AF=AB，EF=BE．所以矩形的周长等于△AFD和△CFE的周长的和为9+3=12．故矩形ABCD的周长为12．
点评：本题利用了折叠的性质．
解答：解：由折叠的性质知，AF=AB，EF=BE．所以矩形的周长等于△AFD和△CFE的周长的和为9+3=12．故矩形ABCD的周长为12．
点评：本题利用了折叠的性质．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
23、如图，将矩形纸片ABCD沿EF折叠，使点A与点C重合，点D落在点G处，EF为折痕．
（2013•松北区三模）如图，将矩形纸片ABCD折痕，使点D落在点线段AB的中点F处．若AB=4，则边BC的长为（ ）
如图，将矩形纸片ABCD沿其对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E．
