题目内容
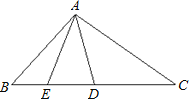
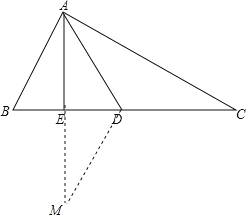
【题目】已知:如图,D是△ABC的边BC上的一点,且CD=AB,∠BDA=∠BAD,AE是△ABD的中线.
⑴若∠B=60°,求∠C的值;
⑵求证:AD是∠EAC的平分线.
【答案】(1)∠C=30°;(2)详见解析.
【解析】
(1)根据已知条件得到∠BAD=∠BDA=60°,于是得到AB=AD,等量代换得到CD=AD,根据等腰三角形的性质得到∠DAC=∠C,推出∠BDA=∠DAC+∠C=2∠C,即可得到结论;
(2)证明:延长AE到M,使EM=AE,连接DM,推出△ABE≌△MDE,根据全等三角形的性质得到∠B=∠MDE,AB=DM,根据全等三角形的判定定理得到△MAD≌△CAD,根据全等三角形的性质得到∠MAD=∠CAD于是得到结论.
(1)∵∠B=60°,∠BDA=∠BAD,
∴∠BAD=∠BDA=60°,
∴AB=AD,
∵CD=AB,
∴CD=AD,
∴∠DAC=∠C,
∴∠BDA=∠DAC+∠C=2∠C,
∵∠BAD=60°,
∴∠C=30°;
(2)证明:延长AE到M,使EM=AE,连接DM,
在△ABE和△MDE中,
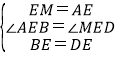 ,
,
∴△ABE≌△MDE,
∴∠B=∠MDE,AB=DM,
∵∠ADC=∠B+∠BAD=∠MDE+∠BDA=∠ADM,
在△MAD与△CAD,
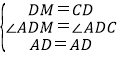 ,
,
∴△MAD≌△CAD,
∴∠MAD=∠CAD,
∴AD是∠EAC的平分线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小亮与小明做投骰子(质地均匀的正方体)的实验与游戏.
(1)在实验中他们共做了50次试验,试验结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 10 | 9 | 6 | 9 | 8 | 8 |
①填空:此次实验中,“1点朝上”的频率是 ;
(2)在游戏时两人约定:每次同时掷两枚骰子,如果两枚骰子的点数之和超过6,则小亮获胜,否则小明获胜.则小亮与小明谁获胜的可能性大?试说明理由.