题目内容

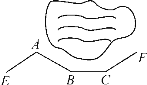
【题目】如图，一条公路绕湖而过，测得三个拐弯的角度分别为∠A＝120°，∠B＝150°，∠C＝150°，试判断公路AE与CF是否平行，并说明理由．

【答案】AE∥CF.

【解析】

延长CB交AE于点D，先由邻补角定义得出∠ABD的度数，再由三角形内角和定理求得∠BDA，从而得到∠BDE，即∠BDE＝∠C，由内错角相等，两直线平行可得AE∥CF.

AE∥CF.

理由：延长CB交AE于点D，

∵∠ABC＝150°，

∴∠ABD＝180°－∠ABC =180°-150°=30°，

∵∠A＝120°，

∴∠BDA＝180°－∠A－∠ABD＝180°－120°－30°＝30°，

∴∠BDE＝180°－∠BDA =180°－30°=150°，

∴∠BDE＝∠C，

∴AE∥CF

练习册系列答案
相关题目

【题目】某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行加价收费，为更好地做决策，自来水公司随机抽取部分用户的用水量数据，并绘制了如图不完整的统计图（每组数据包括最大值但不包括最小值），请你根据统计图解决下列问题：

（1）此次抽样调查的样本容量是　 　

（2）补全左侧统计图，并求扇形统计图中“25吨～30吨”部分的圆心角度数．

（3）如果自来水公司将基本用水量定为每户25吨，那么该地区6万用户中约有多少用户的用水全部享受基本价格？

【题目】已知：如图，D是△ABC的边BC上的一点，且CD=AB，∠BDA=∠BAD，AE是△ABD的中线．

⑴若∠B=60°,求∠C的值；

⑵求证：AD是∠EAC的平分线．

【题目】如图，△ABC中，CD是∠ACB的角平分线，CE是AB边上的高，若∠A=40°，∠B=72°．

（1）求∠DCE的度数；

（2）试写出∠DCE与∠A、∠B的之间的关系式．（不必证明）

【题目】为深化义务教育课程改革，某校积极开展拓展性课程建设，计划开设艺术、体育、劳技、文学等多个类别的拓展性课程，要求每一位学生都自主选择一个类别的拓展性课程．为了了解学生选择拓展性课程的情况，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图（部分信息未给出）：

根据统计图中的信息，解答下列问题：

（）求本次被调查的学生人数．

（）将条形统计图补充完整．

（）若该校共有名学生，请估计全校选择体育类的学生人数．

【题目】（10分）某工厂计划在规定时间内生产24000个零件，若每天比原计划多生产30个零件，则在规定时间内可以多生产300个零件．

（1）求原计划每天生产的零件个数和规定的天数．

（2）为了提前完成生产任务，工厂在安排原有工人按原计划正常生产的同时，引进5组机器人生产流水线共同参与零件生产，已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%，按此测算，恰好提前两天完成24000个零件的生产任务，求原计划安排的工人人数．

【题目】某班共有52名同学，在校广播操比赛中排成方队，先把每位同学都进行编号，然后把各自的位置固定下来，如图，在平面直角坐标系中，每个自然数都对应着一个坐标．例如1的对应点是原点，3的对应点是，16的对应点是．那么最后一名同学的位置对应的坐标是____，全校学生如果排成这样一个大方阵，编号是2015的学生的对应点的坐标是___．

【题目】探究题：

（1）三条直线相交，最少有__________个交点，最多有__________个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；

（2）四条直线相交，最少有__________个交点，最多有__________个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；

（3）依次类推，n条直线相交，最少有__________个交点，最多有__________个交点，对顶角有__________对，邻补角有__________对.

【题目】如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（　　）

A. 1 B. C. D. 4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网