题目内容
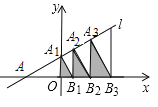
【题目】如图,![]() 为等边三角形,
为等边三角形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() .
.
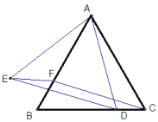
(1)求证:![]() ;
;
(2)以![]() 为边作等边三角形
为边作等边三角形![]() ,点
,点![]() 在线段
在线段![]() 上的何处时,四边形
上的何处时,四边形![]() 是平行四边形且
是平行四边形且![]() .
.
【答案】(1)见解析;(2)D在线段BC上的中点,四边形CDEF是平行四边形,理由见解析.
【解析】
(1)在△ACD和△CBF中,根据已知条件有两边和一夹角对应相等,可根据边角边来证明全等.
(2)当![]() ,即为∠DCF=30
,即为∠DCF=30![]() ,在△BCF中,∠CFB=90
,在△BCF中,∠CFB=90![]() ,即F为AB的中点,又因为△ACD≌△CBF,所以点D为BC的中点.
,即F为AB的中点,又因为△ACD≌△CBF,所以点D为BC的中点.
(1)由△ABC为等边三角形,AC=BC,∠FBC=∠DCA,
在△ACD和△CBF中,
 ,
,
所以△ACD≌△CBF(SAS);
(2)当D在线段BC上的中点时,四边形CDEF为平行四边形,且角DEF=30度
按上述条件作图,
连接BE,

在△AEB和△ADC中,
AB=AC,∠EAB+∠BAD=∠DAC+∠BAD=60![]() ,即∠EAB=∠DAC,AE=AD,
,即∠EAB=∠DAC,AE=AD,
∴△AEB≌△ADC(SAS),
又∵△ACD≌△CBF,
∴△AEB≌△ADC≌△CFB,
∴EB=FB,∠EBA=∠ABC=60![]() ,
,
∴△EFB为正三角形,
∴EF=FB=CD,∠EFB=60![]() ,
,
又∵∠ABC=60![]() ,
,
∴∠EFB=∠ABC=60![]() ,
,
∴EF∥BC,
而CD在BC上,
∴EF平行且相等于CD,
∴四边形CDEF为平行四边形,
∵D在线段BC上的中点,
∴F在线段AB上的中点,
∴∠FCD=![]() ×60
×60![]() =30
=30![]()
则∠DEF=∠FCD=30![]()
∴当D在线段BC上的中点时,四边形CDEF为平行四边形,且![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目