题目内容
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在 轴上,点C1、E1、E2、C2、E3、E4、C3在
轴上,点C1、E1、E2、C2、E3、E4、C3在 轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60º,B1C1∥B2C2∥B3C3,则点A3到
轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60º,B1C1∥B2C2∥B3C3,则点A3到 轴的距离是( )
轴的距离是( )

 轴上,点C1、E1、E2、C2、E3、E4、C3在
轴上,点C1、E1、E2、C2、E3、E4、C3在 轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60º,B1C1∥B2C2∥B3C3,则点A3到
轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60º,B1C1∥B2C2∥B3C3,则点A3到 轴的距离是( )
轴的距离是( )
A. | B. | C. | D.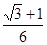 |
D
试题分析:利用正方形的性质以及平行线的性质可分别得出D1E1、B2E2、B2C2的长,进而得出B3C3、WQ的长,最后根据30°的余弦函数求解即可.
过小正方形的一个顶点W作FQ⊥x轴于点Q,过点A3F⊥FQ于点F,
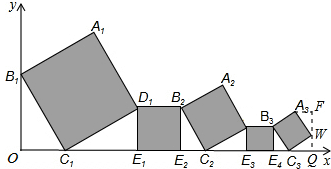
∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,
∴∠B3C3 E4=60°,∠D1C1E1=30°,∠E2B2C2=30°,
∴D1E1=
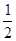 D1C1=
D1C1=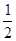 ,
,∴D1E1=B2E2=
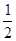 ,
,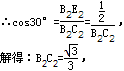
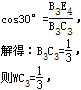
根据题意得出:∠WC3 Q=30°,∠C3 WQ=60°,∠A3 WF=30°,

故选D.
点评:本题综合性强,难度较大,是中考常见题,一般出现在选择、填空的最后一题.

练习册系列答案
相关题目
 ,则菱形ABCD的面积是__________
,则菱形ABCD的面积是__________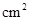 .
.

 ,连接DE并延长交AB于M,连接BF交CD于N,
,连接DE并延长交AB于M,连接BF交CD于N,
 的值.
的值. ,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③
,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③ ;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。
;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。
