题目内容
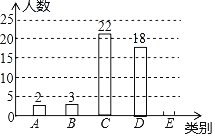
【题目】某校响应国家号召,鼓励学生积极参与体育锻炼.为了解学生一星期参与体育锻炼的时间情况,从全校2000名学生中,随机抽取50名学生进行调查,按参与体育锻炼的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:
(1)样本中E类学生有 人,补全条形统计图;
(2)估计全校的D类学生有 人;
(3)从该样本参与体育锻炼时间在0≤t≤4的学生中任选2人,求这2人参与体育锻炼时间都在2<t≤4中的概率.
【答案】(1)5,见解析;(2)720;(3)![]()
【解析】
(1)根据总人数等于各类别人数之和可得E类别学生数;
(2)用D类别学生数除以总人数即可得D类人数占被调查人数的百分比,再乘以总人数2000即可得;
(3)列举所有等可能结果,根据概率公式求解可得.
解:(1)E类学生有50﹣(2+3+22+18)=5(人),
补全图形如下:
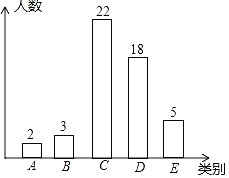
故答案为:5;
(2)D类学生人数占被调查总人数的![]() ×100%=36%,
×100%=36%,
所以估计全校的D类学生有2000×36%=720(人);
故答案为:720;
(3)记0≤t≤2内的两人为甲、乙,2<t≤4内的3人记为A、B、C,
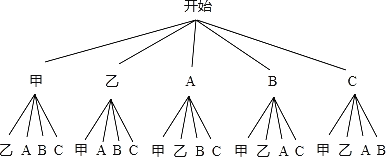
从中任选两人有20种可能结果,
其中2人锻炼时间都在2<t≤4中的有AB、AC、BC这6种结果,
∴这2人锻炼时间都在2<t≤4中的概率为![]() .
.

练习册系列答案
相关题目