题目内容
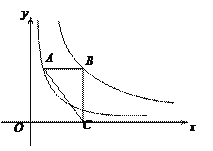
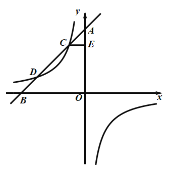
【题目】如图所示,一次函数y=k1x+8的图像与坐标轴分别相较于点A,B与反比例y=![]() 函数的图像相交于C,D.过点C作CE⊥y轴,垂足为E.且CE=2.
函数的图像相交于C,D.过点C作CE⊥y轴,垂足为E.且CE=2.
(1)求4k1-k2的值;
(2)若CD=2AC,求反比例函数的解析式.
【答案】(1)16;(2)y=﹣![]()
【解析】
(1)利用C点的横坐标为﹣2得到C点的纵坐标可表示为﹣2k1+8或﹣![]() ,则﹣2k1+8=﹣
,则﹣2k1+8=﹣![]() ,然后变形得到4k1﹣k2=16;
,然后变形得到4k1﹣k2=16;
(2)作DF⊥y轴于F,如图,利用平行线分线段成比例定理得到![]() ,解得DF=6,与(1)中的方法一样表示出D的纵坐标,所以36k1﹣k2=48,然后通过解方程组求出k2,从而得到反比例函数解析式.
,解得DF=6,与(1)中的方法一样表示出D的纵坐标,所以36k1﹣k2=48,然后通过解方程组求出k2,从而得到反比例函数解析式.
解:(1)∵CE=2,
∴C点的横坐标为﹣2,
当x=﹣2时,y=k1x+8=﹣2k1+8;
当x=﹣2时,y=![]() =﹣
=﹣![]() ,
,
∴﹣2k1+8=﹣![]()
∴4k1﹣k2=16;
(2)作DF⊥y轴于F,如图,
∵CE∥DF,
∴![]() ,
,
而CD=2AC,
∴![]() =
=![]() ,解得DF=6,
,解得DF=6,
当x=﹣6时,y=k1x+8=﹣6k1+8;
当x=﹣6时,y=![]() =﹣
=﹣![]()
∴﹣6k1+8=﹣![]() ,
,
∴36k1﹣k2=48,
∵4k1﹣k2=16;
∴k1=1,k2=﹣12,
∴反比例函数解析式为y=﹣![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目