Question

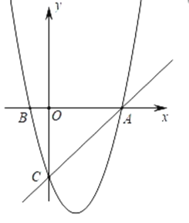
【题目】如图，在平面直角坐标系中，已知抛物线y＝x2+bx+c过A，B，C三点，点A的坐标是(3，0)，点C的坐标是(0，﹣3)，动点P在抛物线上．

（1）b＝　 　，c＝　 　，点B的坐标为　 　；

（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；

（3）是否存在点P使得∠PCA＝15°，若存在，请直接写出点P的横坐标．若不存在，请说明理由．

Answer 1

【答案】（1）﹣2，﹣3，(﹣1，0)；（2）存在，(1，﹣4)或(﹣2，5)；（3）存在，或

【解析】

（1）将点A、C的坐标代入抛物线表达式，即可求解；

（2）分∠ACP是直角、∠P′AC为直角两种情况，分别求解即可；

（3）分点P在直线AC下方、P（P′）在直线AC的上方两种情况，分别求解即可．

（1）将点A、C的坐标代入抛物线表达式得：，解得：，

故抛物线的表达式为：y＝x2﹣2x﹣3①，

令y＝0，则x＝3或﹣1，故点B（﹣1，0）；

故答案为：﹣2，﹣3，（﹣1，0）；

（2）存在，

理由：如图1所示：

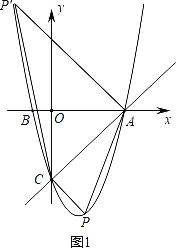
当①∠ACP是直角时，

由点A、C的坐标知，OC＝OA，即∠ABC＝45°，

则PC与x轴的夹角为45°，

则设PC的表达式为：y＝﹣x﹣3②，

联立①②并解得：x＝0或1（舍去0），

故点P（1，﹣4）；

②当∠P′AC为直角时，

同理可得：点P′的坐标为：（﹣2，5）；

综上所述，P的坐标是（1，﹣4）或（﹣2，5）；

（3）存在，

理由：如图2所示，

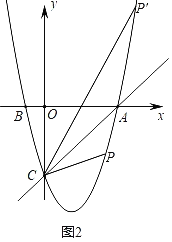
①当点P在直线AC下方时，

由（2）知：∠OCA＝45°，

又∵∠PCA＝15°，

∴∠OCP＝45°+15°＝60°，

即直线PC的倾斜角为30°，

则直线PC的表达式为：y＝x﹣3③，

联立①③并解得：x＝2+或0（舍去0）；

故x＝2+；

②当点P（P′）在直线AC的上方时，

同理可得：点P的横坐标为：2+；

综上，点P的横坐标是：或．