题目内容
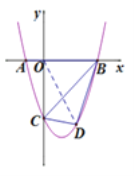
【题目】如图(1),抛物线y=ax2+bx+c与x轴交于A(x1,0)、B(x2,0)两点(x1<0<x2),与y轴交于点C(0,-3),若抛物线的对称轴为直线x=1,且tan∠OAC=3.
(1)求抛物线的函数解析式;
(2 若点D是抛物线BC段上的动点,且点D到直线BC距离为![]() ,求点D的坐标
,求点D的坐标
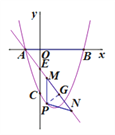
(3)如图(2),若直线y=mx+n经过点A,交y轴于点E(0, -![]() ),点P是直线AE下方抛物线上一点,过点P作x轴的垂线交直线AE于点M,点N在线段AM延长线上,且PM=PN,是否存在点P,使△PMN的周长有最大值?若存在,求出点P的坐标及△PMN的周长的最大值;若不存在,请说明理由.
),点P是直线AE下方抛物线上一点,过点P作x轴的垂线交直线AE于点M,点N在线段AM延长线上,且PM=PN,是否存在点P,使△PMN的周长有最大值?若存在,求出点P的坐标及△PMN的周长的最大值;若不存在,请说明理由.

【答案】(1)![]() ;(2)D1(1,-4),D2(2,-3);(3)存在,
;(2)D1(1,-4),D2(2,-3);(3)存在, ![]() ,△PMN的周长的最大值是
,△PMN的周长的最大值是![]()
【解析】试题分析:(1)根据题意求出A,B两点坐标,设解析式为交点式,代入点C即可求出;(2)设D(x,x-2x-3),根据三角形BCD的面积即可求出D点坐标;(3)求出直线AE的表达式,设P(t,t-2t-3),用含t的式子表示出PM=PN的长度,利用![]() ∽△AEO表示出MN的长度,从而三角形的周长就可以用含t的二次函数来表示,根据二次函数的性质即可求出P的坐标和△PMN的周长的最大值.
∽△AEO表示出MN的长度,从而三角形的周长就可以用含t的二次函数来表示,根据二次函数的性质即可求出P的坐标和△PMN的周长的最大值.
试题解析:
(1)在Rt△AOC中,tan∠OAC=![]() =3,且OC=3,∴OA=1,A(-1,0).
=3,且OC=3,∴OA=1,A(-1,0).
∵抛物线的对称轴为直线x=1,
∴由中点坐标公式可求; ![]() ,解得x=3.
,解得x=3.
∴B(3,0).
∴可设抛物线的表达式为:y=a(x-3)(x+1)
将C(0,-3)代入上式中, ![]()
∴抛物线表达式为:y=(x-3)(x+1)=x-2x-3.
(3)∵B(3,0)、C(0,-3),
∴BC=![]()
∴![]()
设D(x,x-2x-3),连接OD,
∴![]()
=![]()
=![]()
=![]() .
.
解得x=1, x=2.
∴D(1,-4),(2,-3).
(3)由A(-1,0)、E(0, ![]() )可求:
)可求:
直线AE的表达式为:  .
.
设P(t,t-2t-3),则![]()
∴![]() .
.
作PG⊥MN于G,由PM=PN得:MG=NG=![]() MN,
MN,
由![]() ∽△AEO 有:
∽△AEO 有: ![]() ,即
,即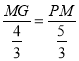
∴MG=![]() PM=NG
PM=NG
∴![]()
∴当![]() ,
,![]() 有最大值为
有最大值为![]() ,此时
,此时![]() .
.
点睛:此题以二次函数为背景,综合考查相似三角形的判定与性质,三角形的周长,二次函数的最值,方程思想,函数思想,转化思想等数学知识与数学思想方法,综合性较强.本题通过![]() 与△AEO之间的相似关系,运用相似三角形的性质,用函数关系式表示出△PMN的周长是解答此题的关键.
与△AEO之间的相似关系,运用相似三角形的性质,用函数关系式表示出△PMN的周长是解答此题的关键.

【题目】为保证中小学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的频率统计表和频数分布直方图.请你根据图表信息完成下列各题:
(1)填空: a= ;m= ;n= ;
(2)请将条形统计图补充完整;
(3)该校共有学生1500人,估计参加乒乓球项目的学生有 人;
运动项目 | 频数(人数) | 频率 |
篮球 | 20 | 0.40 |
乒乓球 | n | 0.10 |
足球 | 10 | m |
其他 | 15 | 0.30 |
合计 | a | 1.00 |
